��Ŀ����
����Ŀ��ij������ij��Ʒ����̶��ɱ�Ϊ250��Ԫ��ÿ����![]() ǧ��������Ͷ��ɱ�
ǧ��������Ͷ��ɱ�![]() ����Ԫ���������������
����Ԫ���������������![]() ǧ����
ǧ���� ![]() ��ͼ������ͼ�������ߣ���ʱ
��ͼ������ͼ�������ߣ���ʱ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ����
����![]() ����Сֵ��
����Сֵ��![]() �����������С��
�����������С��![]() ǧ����
ǧ���� ![]() ��ÿǧ����Ʒ�ۼ�Ϊ50��Ԫ��ͨ���г��������ó���������Ʒ��ȫ�����ꣻ
��ÿǧ����Ʒ�ۼ�Ϊ50��Ԫ��ͨ���г��������ó���������Ʒ��ȫ�����ꣻ
��1��д��������![]() ����Ԫ�����������
����Ԫ�����������![]() ��ǧ�����ĺ�������ʽ��
��ǧ�����ĺ�������ʽ��
��2�������Ϊ����ǧ��ʱ���ó�����һ��Ʒ�������������������

���𰸡�(1) 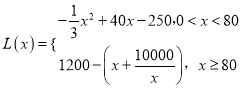 (2) �������
(2) �������![]() ǧ��ʱ���ó�����һ��Ʒ�������������������Ϊ
ǧ��ʱ���ó�����һ��Ʒ�������������������Ϊ![]() ��Ԫ.
��Ԫ.
�������������������1�������֪������=�ۼ�-�ɱ����ֱ�����������![]() �����Լ��������С��
�����Լ��������С��![]() �����㣬���벻ͬ����Ľ���ʽ���������
�����㣬���벻ͬ����Ľ���ʽ���������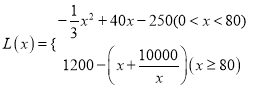 ��
��
��2���ֱ�������������![]() �����Լ��������С��
�����Լ��������С��![]() �����������������80��ʱ�����䷽�������������ֵΪ950��Ԫ�����������С��
�����������������80��ʱ�����䷽�������������ֵΪ950��Ԫ�����������С��![]() ��ʱ���ɾ�ֵ����ʽ����������ֵΪ1000��Ԫ���������Ϊ
��ʱ���ɾ�ֵ����ʽ����������ֵΪ1000��Ԫ���������Ϊ![]() ��ʱ���������Ϊ
��ʱ���������Ϊ![]() ��Ԫ��
��Ԫ��
�����������1����![]() ʱ��
ʱ�� ![]()
![]() ��
��
��![]() ʱ��
ʱ�� ![]()
![]() ��
��
����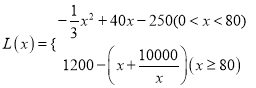 ��
��![]() ����
����
��2����![]() ʱ��
ʱ�� ![]()
��ʱ����![]() ʱ��
ʱ�� ![]() ȡ�����ֵ
ȡ�����ֵ![]() ��Ԫ��
��Ԫ��
��![]() ʱ��
ʱ�� ![]()
��ʱ����![]() ʱ����
ʱ����![]() ʱ��
ʱ�� ![]() ȡ�����ֵ
ȡ�����ֵ![]() ��Ԫ��
��Ԫ�� ![]()
���������Ϊ![]() ��ʱ���������Ϊ
��ʱ���������Ϊ![]() ��Ԫ��
��Ԫ��