题目内容
函数y=(
)x2-3x+2的单调递增区间为 ．
| 1 |
| 3 |
考点：指数型复合函数的性质及应用
专题：计算题,函数的性质及应用
分析：利用复合函数的单调性判断函数的单调区间．
解答：
解：∵y=x2-3x+2在（-∞，
]上是减函数，
在（
，+∞）上是增函数；
又∵y=(
)x在R上是减函数；
故函数y=(
)x2-3x+2的单调递增区间为（-∞，
]；
故答案为：（-∞，
]．
| 3 |
| 2 |
在（
| 3 |
| 2 |
又∵y=(
| 1 |
| 3 |
故函数y=(
| 1 |
| 3 |
| 3 |
| 2 |
故答案为：（-∞，
| 3 |
| 2 |
点评：本题考查了复合函数的单调性的判断，属于基础题．
练习册系列答案
相关题目
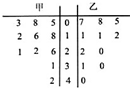某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们在这11场比赛的得分用下面的茎叶图表示，设甲运动员得分的中位数为M1，乙运动员得分的中位数为M2，则在下列选项中，正确的是（ ）| A、M1=18，M2=11 |
| B、M1=81，M2=12 |
| C、M1=8，M2=2 |
| D、M1=3，M2=1 |
圆x2+y2+2x-4y=0的半径为（ ）
| A、3 | ||
B、
| ||
C、
| ||
| D、5 |
已知函数f（x）是定义在R上的偶函数，且对任意的x1、x2∈[0，+∞），x1≠x2，恒有
＞0成立，则以下结论正确的是（ ）
| f(x2)-f(x1) |
| x2-x1 |
| A、f（2）＞f（-1）＞f（-3） |
| B、f（2）＞f（-3）＞f（-1） |
| C、f（-3）＞f（2）＞f（-1） |
| D、f（-3）＞f（-1）＞f（2） |