题目内容
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (
( 为参数).
为参数).
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为 ,判断点P与直线
,判断点P与直线 的位置关系;
的位置关系;
(2)设点Q是曲线C上的一个动点,求点Q到直线 的距离的最小值与最大值.
的距离的最小值与最大值.
(1)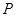 不在直线
不在直线 上;(2)最小值为
上;(2)最小值为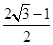 ,最大值为
,最大值为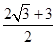 .
.
解析试题分析:(1)消去参数,将直线的参数方程化为普通方程,利用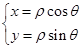 ,再将点
,再将点 的极坐标化为直角坐标,再判断点
的极坐标化为直角坐标,再判断点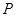 的坐标是否满足方程,进而判断点和直线的位置关系;(2)设点
的坐标是否满足方程,进而判断点和直线的位置关系;(2)设点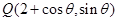 ,利用点到直线的距离公式表示点Q到直线
,利用点到直线的距离公式表示点Q到直线 的距离
的距离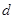 ,转化为三角函数的最值问题处理.
,转化为三角函数的最值问题处理.
试题解析:(Ⅰ)将点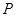
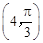 化为直角坐标,得
化为直角坐标,得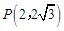 ,直线
,直线 的普通方程为
的普通方程为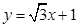 ,显然点
,显然点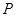 不满足直线
不满足直线 的方程,所以点
的方程,所以点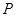 不在直线
不在直线 上.
上.
(Ⅱ)因为点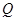 在曲线
在曲线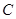 上,故可设点
上,故可设点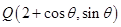 ,点
,点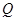 到直线
到直线 :
: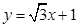 的距离为
的距离为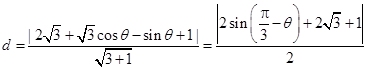 ,所以当
,所以当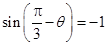 时,
时,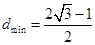 ,
,
当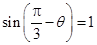 时,
时,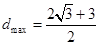 .故点
.故点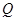 到直线
到直线 的距离的最小值为
的距离的最小值为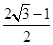 ,最大值为
,最大值为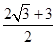 .
.
考点:1直线参数方程和普通方程的互化;2、极坐标和直角坐标的互化;3、点到直线的距离.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的参数方程是
的参数方程是 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线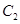 的极坐标方程是
的极坐标方程是 .
. 、
、 的极坐标分别是
的极坐标分别是 、
、 ,直线
,直线 与曲线
与曲线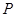 、
、 两点,射线
两点,射线 与曲线
与曲线 ,射线
,射线 与曲线
与曲线 ,求
,求 的值.
的值. )=
)= ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0, 的方程为
的方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数),若直线
为参数),若直线 的值.
的值. ,半径R=
,半径R= ,求圆C的极坐标方程.
,求圆C的极坐标方程. (
( 为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点
为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点 ,直线
,直线 的极坐标方程为
的极坐标方程为 .
. 与直线
与直线 的值.
的值. (
( ,
, 为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1,
为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心在极轴上,且经过极点的圆.已知曲线C1上的点M(1, )对应的参数j=
)对应的参数j= ,曲线C2过点D(1,
,曲线C2过点D(1, )在曲线C1上,求
)在曲线C1上,求 的值.
的值. 中,曲线
中,曲线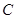 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线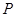 的方程为
的方程为 .
. 、
、 ,求
,求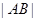 .
. ②
②