题目内容
已知曲线 的参数方程是
的参数方程是 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线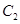 的极坐标方程是
的极坐标方程是 .
.
(1)写出 的极坐标方程和
的极坐标方程和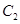 的直角坐标方程;
的直角坐标方程;
(2)已知点 、
、 的极坐标分别是
的极坐标分别是 、
、 ,直线
,直线 与曲线
与曲线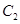 相交于
相交于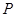 、
、 两点,射线
两点,射线 与曲线
与曲线 相交于点
相交于点 ,射线
,射线 与曲线
与曲线 相交于点
相交于点 ,求
,求 的值.
的值.
(1) :
: ,
, ;(2)
;(2) .
.
解析试题分析:(1)题中参数方程化为普通方程只要消去参数 ,极坐标系与直角坐标系的互化公式为:
,极坐标系与直角坐标系的互化公式为: ;(2)首先明确
;(2)首先明确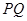 是什么?可把点
是什么?可把点 坐标化为直角坐标,发现
坐标化为直角坐标,发现 就是圆心,从而线段
就是圆心,从而线段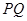 是圆的直径,因此题中有
是圆的直径,因此题中有 ,即
,即 ,我们在极坐标系中证明本题结论较方便,因为可设
,我们在极坐标系中证明本题结论较方便,因为可设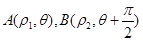 ,代入
,代入 的极坐标方程,可得
的极坐标方程,可得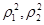 ,代入即可求得
,代入即可求得 .
.
试题解析:(1)曲线 的普通方程为
的普通方程为 1分
1分
化为极坐标方程为: 3分
3分
曲线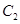 的普通方程为:
的普通方程为: 5分
5分
(2)在直角坐标系下, ,
,
线段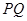 是是圆
是是圆 的一条直径,
的一条直径,
∴ ,由
,由 ,有
,有 6分
6分 是椭圆上的两点,在极坐标系下,设
是椭圆上的两点,在极坐标系下,设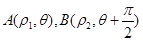 分别代入
分别代入 ,
,
有 ,
, 8分
8分
解得: ,
, .
.
则 9分
9分
即

 . 10分
. 10分
考点:(1)参数方程,极坐标方程与普通方程的互化;(2)极径的计算.

练习册系列答案
相关题目
 ,求:
,求: 中
中 的最大值和最小值.
的最大值和最小值. (
( 为参数),曲线
为参数),曲线 ,将
,将 的横坐标伸长为原来的2倍,纵坐标缩短为原来的
的横坐标伸长为原来的2倍,纵坐标缩短为原来的 得到曲线
得到曲线 .
. 的直角坐标方程;
的直角坐标方程; 的最小值,并求此时的P的坐标.
的最小值,并求此时的P的坐标. .
. ,以极点为原点,极轴所在直线为x轴建立平面直角坐标系.
,以极点为原点,极轴所在直线为x轴建立平面直角坐标系. 的参数方程为
的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (
( 为参数).
为参数). ,判断点P与直线
,判断点P与直线