题目内容
已知α∈(
,π),向量
=(sin
,1),
=(1,cos
),且
•
=
(1)求cosα的值;
(2)若sin(α+β)=-
,β∈(0,
),求sinβ的值.
| π |
| 2 |
| a |
| α |
| 2 |
| b |
| α |
| 2 |
| a |
| b |
2
| ||
| 3 |
(1)求cosα的值;
(2)若sin(α+β)=-
| 3 |
| 5 |
| π |
| 2 |
(1)∵
•
=
,∴sin
+cos
=
,
两边平方得1+2sin
cos
=
,∴sinα=
.
∵α∈(
,π),∴cosα=-
=-
.
(2)∵α∈(
,π),β∈(0,
),
∴(α+β)∈(
,
).
∵sin(α+β)=-
,
∴cos(α+β)=-
=-
.
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα
=(-
)•(-
)-(-
)•
=
.
| a |
| b |
2
| ||
| 3 |
| α |
| 2 |
| α |
| 2 |
2
| ||
| 3 |
两边平方得1+2sin
| α |
| 2 |
| α |
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
∵α∈(
| π |
| 2 |
| 1-sin2α |
2
| ||
| 3 |
(2)∵α∈(
| π |
| 2 |
| π |
| 2 |
∴(α+β)∈(
| π |
| 2 |
| 3π |
| 2 |
∵sin(α+β)=-
| 3 |
| 5 |
∴cos(α+β)=-
| 1-sin2(α+β) |
| 4 |
| 5 |
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα
=(-
| 3 |
| 5 |
2
| ||
| 3 |
| 4 |
| 5 |
| 1 |
| 3 |
=
6
| ||
| 15 |

练习册系列答案
相关题目
 已知定点A
已知定点A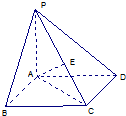 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知:PA=2,AB=2,
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知:PA=2,AB=2,