题目内容
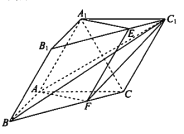
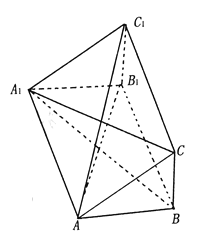
【题目】在如图所示的几何体中,四边形![]() 是等腰梯形,
是等腰梯形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() .
.
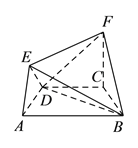
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
(![]() )在线段
)在线段![]() (含端点)上,是否存在一点
(含端点)上,是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(![]() )见解析;(
)见解析;(![]() )
)![]() ;(
;(![]() )存在,
)存在, ![]()
【解析】试题分析:(1)由题意,证明![]() ,
, ![]() ,证明
,证明![]() 面
面![]() ;(2)建立空间直角坐标系,求平面
;(2)建立空间直角坐标系,求平面![]() 和平面
和平面![]() 的法向量,解得余弦值为
的法向量,解得余弦值为![]() ;(3)得
;(3)得![]() ,
, 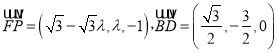 ,所以
,所以![]() ,
, ![]() ,所以存在
,所以存在![]() 为
为![]() 中点.
中点.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() .
.
∵![]() ,且
,且![]() ,
,
![]() 、
、![]() 面
面![]() ,∴
,∴![]() 面
面![]() .
.
(![]() )知
)知![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,
以![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴建系.
轴建系.
设![]() ,则
,则![]() ,
, ![]() ,
,  ,
, ![]() ,
, ![]() ,
,
∴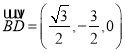 ,
, ![]() .
.
设![]() 的一个法向量为
的一个法向量为![]() ,
,
∴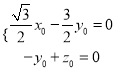 ,取
,取![]() ,则
,则![]() .
.
由于![]() 是面
是面![]() 的法向量,
的法向量,
则 .
.
∵二面角![]() 为锐二面角,∴余弦值为
为锐二面角,∴余弦值为![]() .
.
(![]() )存在点
)存在点![]() .
.
设![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 面
面![]() ,
, 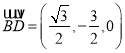 .
.
若![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴存在
,∴存在![]() 为
为![]() 中点.
中点.

【题型】解答题
【结束】
19
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求此函数对应的曲线在
时,求此函数对应的曲线在![]() 处的切线方程.
处的切线方程.
(![]() )求函数
)求函数![]() 的单调区间.
的单调区间.
(![]() )对
)对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(![]() )
)![]() ;(
;(![]() )见解析;(
)见解析;(![]() )当
)当![]() 时,
时, ![]() ,当
,当![]() 时
时![]()
【解析】试题分析:(1)利用导数的意义,求得切线方程为![]() ;(2)求导得
;(2)求导得![]() ,通过
,通过![]() ,
, ![]() ,
, ![]() 分类讨论,得到单调区间;(3)分离参数法,得到
分类讨论,得到单调区间;(3)分离参数法,得到![]() ,通过求导,得
,通过求导,得![]() ,
, ![]() .
.
试题解析:
(![]() )当
)当![]() 时,
时, ![]() ,
,
∴![]() ,
, ![]() ,
,
![]() ,∴切线方程
,∴切线方程![]() .
.
(![]() )
)![]()
![]()
![]() .
.
令![]() ,则
,则![]() 或
或![]() ,
,
当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上为增函数.
上为增函数.
在![]() 上为减函数,
上为减函数,
当![]() 时,
时, ![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上为单调递增,
上为单调递增,
在![]() 上单调递减.
上单调递减.
(![]() )当
)当![]() 时,
时, ![]() ,
,
当![]() 时,由
时,由![]() 得
得
![]() ,对
,对![]() 恒成立.
恒成立.
设![]() ,则
,则
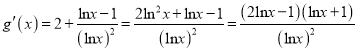 ,
,
令![]() 得
得![]() 或
或![]() ,
,
|
|
|
|
|
|
|
|
|
| 极小 |
|
![]() ,∴
,∴![]() ,
, ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目