题目内容
设等比数列 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为
 2
2
解析试题分析:设等比数列{an}的公比为q,前n项和为Sn,且Sn+1,Sn,Sn+2成等差数列,则2Sn=Sn+1+Sn+2 .
若q=1,则Sn=na1,式显然不成立.
若q≠1,则 =
= +
+
故2qn=qn+1+qn+2,即q2+q-2=0,因此q=-2.
考点:本题主要考查等差数列的定义和性质,等比数列的前n项和公式。
点评:涉及等比数列求和时,若公比为字母,则需要分类讨论,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数 对应关系如表1所示,数列
对应关系如表1所示,数列 满足
满足 ,
, ,则
,则 .
.
 | 1 | 2 | 3 |
 | 3 | 2 | 1 |
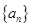 中,
中, ,则公比
,则公比 ;
; 中,首项
中,首项 ,前3项和为14,则
,前3项和为14,则 值为_____________.
值为_____________. 中
中 ,且
,且 ,则
,则 =
=  满足:
满足: ,若存在两项
,若存在两项 ,使得
,使得

 的最小值为
的最小值为  中,有
中,有
 的左、右顶点分别是
的左、右顶点分别是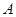 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 .若
.若 ,
, ,
, 成等比数列,求此椭圆的离心率.
成等比数列,求此椭圆的离心率. 中,
中, 若
若 ,则
,则 = .
= .