题目内容
设椭圆
的左、右焦点分别为
.
是椭圆上的一点，
，原点
到直线
的距离为
；
（1）求椭圆的离心率；
（2）若左焦点
设过点
且不与坐标轴垂直的直线交椭圆于
两点，线段
的垂直平分线与x轴交于
，求点横坐标的取值范围.
（1）
（2）
解析:
（1）解法1：由题设AF2⊥F1F2，及F1（－c,0），F2（c,0），不妨设点A（c,y），其中y>0.
由于点A在椭圆上，有
即
.……………………2分
直线AF1的方程为
由题设，原点O到直线AF1的距离为
…………4分
将
，进而求得……6分
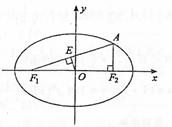
解法2：设O到直线AF1的垂足为E，则
Rt△OEF1—Rt△AF2F1，
（*）……………………2分
由已知条件可求得
………………3分
又
…………4分
代入（*）式得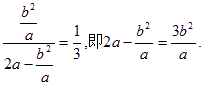
将
代入并化简，得
进而求得…………6分
（2）∵左焦点F1（－1，0）
∴椭圆的方程为
……………… 7分
设直线BC的方程为
代入椭圆方程并整理得
|
记B
则
…………………10分
∴BC的垂直平分线NG的方程为
…………… 11分
令y=0得
…………12分
……………13分
即点G横坐标的取值范围为 ……………14分
练习册系列答案
相关题目
的左、右焦点分别是
、
，离心率
，右准线
上的两动点
、
，且
．
，求
、
的值；
最小时，求证
与
共线．
的离心率
，以原点为圆心，椭圆的短半轴长为半径的圆与直线
相切。（I）求a与b；（II）设椭圆的左，右焦点分别是F1和F2，直线
且与x轴垂直，动直线
轴垂直，
于点P，求线段PF1的垂直平分线与
的交点M的轨迹方程，并指明曲线类型。
的左、右焦点分别是F1、F2，离心率
，右准线l上的两动点M、N，且
，
，求a、b的值；
最小时，求证
与
共线。 
，以原点为圆心，椭圆的短半轴长为半径的圆与直线y=x+2相切．