题目内容
11.函数f(x)=Asin(ωx-$\frac{π}{6}$)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为$\frac{π}{2}$.(1)求函数f(x)的解析式;
(2)设α∈(0,$\frac{π}{2}$),f($\frac{α}{2}$)=2,求α的值;
(3)当x∈(0,$\frac{π}{2}$]时,求f(x)的取值范围.
分析 (1)通过函数的最大值求出A,通过对称轴求出周期,求出ω,得到函数的解析式.
(2)通过$f(\frac{α}{2})=2$,求出$sin(α-\frac{π}{6})\;=\frac{1}{2}$,通过α的范围,求出α的值.
(3)求出角2x-$\frac{π}{6}$的范围结合三角函数的性质进行求解即可.
解答 解:(1)∵函数f(x)的最大值为3,∴A+1=3,即A=2,
∵函数图象相邻两条对称轴之间的距离为$\frac{π}{2}$,$\frac{T}{2}$=$\frac{π}{2}$,T=π,所以ω=2.
故函数的解析式为y=2sin(2x-$\frac{π}{6}$)+1.
(2)∵$f(\frac{α}{2})=2$,∴$f(\frac{α}{2})=2sin(α-\frac{π}{6})\;+1=2$,
∴$sin(α-\frac{π}{6})\;=\frac{1}{2}$,
∵$α∈(0,\frac{π}{2})$,
∴$-\frac{π}{6}<α-\frac{π}{6}<\;\frac{π}{3}$,
∴$α-\frac{π}{6}=\frac{π}{6}$,
∴$α=\frac{π}{3}$.
(3)若x∈(0,$\frac{π}{2}$],则2x-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$],
∴sin(2x-$\frac{π}{6}$)∈(sin(-$\frac{π}{6}$),sin$\frac{π}{2}$]=(-$\frac{1}{2}$,1],
则2sin(2x-$\frac{π}{6}$)∈(-1,2],2sin(2x-$\frac{π}{6}$)+1∈(0,3],
即函数f(x)的取值范围是(0,3].
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的恒等变换及化简求值,考查计算能力,根据条件求出ω的值是解决本题的关键..

| A. | $\overrightarrow{MC}+\overrightarrow{MB}=\overrightarrow 0$ | B. | $\overrightarrow{MC}+\overrightarrow{AB}=\overrightarrow 0$ | C. | $\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow 0$ | D. | $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow 0$ |
| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
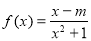 是奇函数,
是奇函数, 是偶函数.
是偶函数.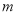 ,
,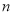 的值;
的值;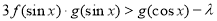 对任意
对任意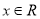 恒成立,求实数
恒成立,求实数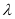 的取值范围.
的取值范围.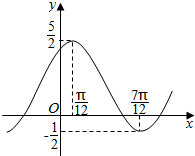 函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)+k(A>0,ω>0,|φ<$\frac{π}{2}$)的图象如图所示.