题目内容
在四棱锥S—ABCD中,∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=a,AD=2a.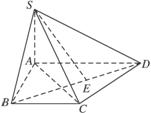
(1)求证:平面SAC⊥平面SCD;
(2)求二面角A-SD-C的大小;
(3)求异面直线SD与AC所成的角;
(4)设E为BD的中点,求SE与平面SAC所成的角.
证明:(1)以A为原点,AB,AD,AS所在直线分别为x,y,z轴建立空间直角坐标系,
∴A(0,0,0),S(0,0,a),C(a,a,0),D(0,2a,0).
∴![]() =(0,0,a),
=(0,0,a),![]() =(-a,-a,a),
=(-a,-a,a),![]() =(-a,a,0).
=(-a,a,0).
∴![]() ·
·![]() =0,
=0,![]() ·
·![]() =0.
=0.
∴CD⊥AS,CD⊥CS.
∴CD⊥平面SAC.
∵CD![]() 平面SCD,
平面SCD,
∴平面SAC⊥平面SCD.
解析:(2)过A作AF⊥SD,过C作CG⊥SD,
则![]() 与
与![]() 的夹角就是二面角的平?面角,
的夹角就是二面角的平?面角,
则F(0,![]() a,
a,![]() a),G(0,
a),G(0,![]() a,
a,![]() a),
a),
∴![]() =(0,-
=(0,-![]() a,-
a,-![]() a),
a),
![]() =(a,-
=(a,-![]() a,-
a,-![]() a).
a).
∴cos,<![]() ,
,![]() >=
>=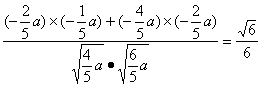 .
.
∴二面角A-SD-C的大小为arccos![]() .
.
(3)![]() =(0,2a,-a),
=(0,2a,-a),![]() =(a,a,0),
=(a,a,0),
∴cos<![]() ,
,![]() >=
>=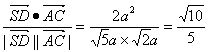 .
.
∴SD与AC所成的角为arccos![]() .
.
(4)∵CD垂直于平面SAC,
∴![]() 为平面SAC的法向量.
为平面SAC的法向量.![]() =(-a,a,0),
=(-a,a,0),
又E为BD的中点,
∴E(![]() ,a,0),
,a,0),
∴![]() =(
=(![]() ,a,-a).
,a,-a).
∴cos<![]() ,
,![]() >=
>=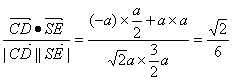 ,
,
∴SE与平面SAC所成的角为![]() -arccos
-arccos![]() .
.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=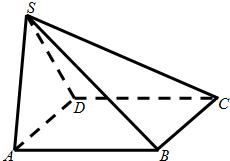 如图,在四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧棱SD=2,SA=2
如图,在四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧棱SD=2,SA=2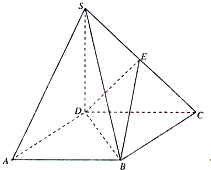 如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是平行四边形,∠BAD=30°,AB=2,
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是平行四边形,∠BAD=30°,AB=2, 如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点. 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,BC=3SA=3AB=3AD.
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,BC=3SA=3AB=3AD.