题目内容
sin22°30′cos22°30′=________.

分析:把所求式子乘以2,再除以2后,利用二倍角的正弦函数公式变形,最后利用特殊角的三角函数值即可求出值.
解答:sin22°30′cos22°30′
=
 ×2sin22°30′cos22°30′
×2sin22°30′cos22°30′=sin(2×22°30′)
=sin45°
=
 .
.故答案为:

点评:此题考查了二倍角的正弦函数公式,以及特殊角的三角函数值,熟练掌握二倍角的正弦函数公式的结构特点是解本题的关键.

练习册系列答案
相关题目
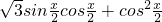 ,当f(B)取最大值
,当f(B)取最大值 时,判断△ABC的形状.
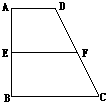
时,判断△ABC的形状. ,AB=BC=2AD=4,E、F分别是两腰AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).
,AB=BC=2AD=4,E、F分别是两腰AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).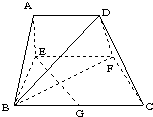
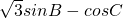 的最大值.
的最大值.
 ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.