题目内容
在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc.
(Ⅰ)求角A的大小;
(Ⅱ)设函数f(x)=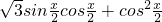 ,当f(B)取最大值
,当f(B)取最大值 时,判断△ABC的形状.
时,判断△ABC的形状.
解:(Ⅰ)在△ABC中,因为b2+c2-a2=bc,由余弦定理a2=b2+c2-2bccosA可得cosA= .
.
∵0<A<π,∴A= .
.
(Ⅱ)函数f(x)=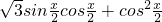 =
= sinx+
sinx+ cosx+
cosx+ =sin(x+
=sin(x+ ),
),
∵A= ,∴B∈( 0,
,∴B∈( 0, ),∴
),∴ <B+
<B+ <
< .
.
∴当B+ =
= ,即 B=
,即 B= 时,f( B)有最大值是
时,f( B)有最大值是 .
.
又∵A= ,∴C=
,∴C= ,∴△ABC为等边三角形.
,∴△ABC为等边三角形.
分析:(Ⅰ)在△ABC中,由余弦定理求得cosA= ,根据 A的范围,求求出 A的大小.
,根据 A的范围,求求出 A的大小.
(Ⅱ)利用二倍角公式化简函数f(x)的解析式为sin(x+ ),再利用角B+
),再利用角B+ 的范围,确定当f(B)取最大值
的范围,确定当f(B)取最大值 时角A和角 C 的大小,从而判断三角形的形状.
时角A和角 C 的大小,从而判断三角形的形状.
点评:本题考查余弦定理的应用,二倍角及两角和差的三角公式的应用.
 .
.∵0<A<π,∴A=
 .
.(Ⅱ)函数f(x)=
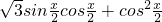 =
= sinx+
sinx+ cosx+
cosx+ =sin(x+
=sin(x+ ),
),∵A=
 ,∴B∈( 0,
,∴B∈( 0, ),∴
),∴ <B+
<B+ <
< .
.∴当B+
 =
= ,即 B=
,即 B= 时,f( B)有最大值是
时,f( B)有最大值是 .
. 又∵A=
 ,∴C=
,∴C= ,∴△ABC为等边三角形.
,∴△ABC为等边三角形.分析:(Ⅰ)在△ABC中,由余弦定理求得cosA=
 ,根据 A的范围,求求出 A的大小.
,根据 A的范围,求求出 A的大小.(Ⅱ)利用二倍角公式化简函数f(x)的解析式为sin(x+
 ),再利用角B+
),再利用角B+ 的范围,确定当f(B)取最大值
的范围,确定当f(B)取最大值 时角A和角 C 的大小,从而判断三角形的形状.
时角A和角 C 的大小,从而判断三角形的形状.点评:本题考查余弦定理的应用,二倍角及两角和差的三角公式的应用.

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|