题目内容
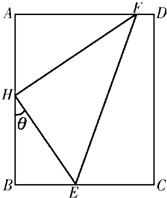 某矩形花园ABCD,AB=2,AD=
某矩形花园ABCD,AB=2,AD=| 3 |
(1)试求S的取值范围;
(2)θ为何值时l的值为最小;并求l的最小值.
分析:(1)要求S的取值范围,我们要先给了S的表达式,由∠BHE为θ,我们易得HE=
,HF=
,且
≤θ≤
,根据三角形面积公式代入给出S的表达式,再结合三角函数的性质,即可求解.
(2)结合(1)中得HE=
,HF=
,
≤θ≤
,根据勾股定理,我们可给出周长l的表达式,化简后根据三角函数的性质即可得到答案.
| 1 |
| cosθ |
| 1 |
| sinθ |
| π |
| 6 |
| π |
| 3 |
(2)结合(1)中得HE=
| 1 |
| cosθ |
| 1 |
| sinθ |
| π |
| 6 |
| π |
| 3 |
解答:解:(1):由图可知在Rt△HBE中有HE=
在Rt△HAF中有HF=
(2分)
由于E在BC上,F在AD上.故
≤θ≤
(4分)
∴S=
HE•HF
=
•
•
=
(6分)
由
≤θ≤
得
≤2θ≤
∴sin2θ∈[
,1]
∴S∈[1,
](9分)
(2)由HE=
,HF=
在Rt△HEF中有FE=
=
∴l=
+
+
=
令sinθ+cosθ=t,则sinθ•cosθ=
(t2-1)
其中t=
sin(θ+
)
∵
≤θ≤
∴
≤θ+
≤
∴
≤sin(θ+
)≤1
∴
≤t≤
l=
=
,
且
≤t≤
当t=
即θ=
时Rt△HEF的周长l最小,最小值为2(
+1)(16分)
| 1 |
| cosθ |
在Rt△HAF中有HF=
| 1 |
| sinθ |
由于E在BC上,F在AD上.故
| π |
| 6 |
| π |
| 3 |
∴S=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| cosθ |
| 1 |
| sinθ |
=
| 1 |
| sin2θ |
由
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴sin2θ∈[
| ||
| 2 |
∴S∈[1,
2
| ||
| 3 |
(2)由HE=
| 1 |
| cosθ |
| 1 |
| sinθ |
在Rt△HEF中有FE=
| HE2+HF2 |
| 1 |
| sinθ•cosθ |
∴l=
| 1 |
| sinθ |
| 1 |
| cosθ |
| 1 |
| sinθ•cosθ |
=
| sinθ+cosθ+1 |
| sinθ•cosθ |
令sinθ+cosθ=t,则sinθ•cosθ=
| 1 |
| 2 |
其中t=
| 2 |
| π |
| 4 |
∵
| π |
| 6 |
| π |
| 3 |
∴
| 5π |
| 12 |
| π |
| 4 |
| 7π |
| 12 |
∴
| ||||
| 4 |
| π |
| 4 |
∴
| ||
| 2 |
| 2 |
| t+1 | ||
|
| 2 |
| t-1 |
且
| ||
| 2 |
| 2 |
当t=
| 2 |
| π |
| 4 |
| 2 |
点评:本题考查的知识点是在实际问题中建立三角函数模型,在解答过程中,根据E在BC上,F在AD上,既定
≤θ≤
,容易被忽略,要引起大家足够的重视!
| π |
| 6 |
| π |
| 3 |

练习册系列答案
相关题目
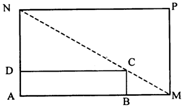 某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.
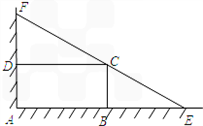
某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.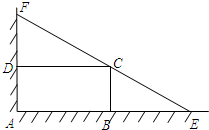 如图,某住宅小区在围墙的墙角处有一矩形绿地ABCD,周围均为荒地,开发商欲把墙角处改造扩建成一个更大的绿地三角形花园AEF,要求EF过点C,若AB长15m,AD长10m.
如图,某住宅小区在围墙的墙角处有一矩形绿地ABCD,周围均为荒地,开发商欲把墙角处改造扩建成一个更大的绿地三角形花园AEF,要求EF过点C,若AB长15m,AD长10m.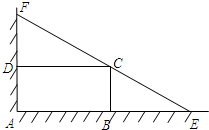 如图,某住宅小区在围墙的墙角处有一矩形绿地ABCD,周围均为荒地,开发商欲把墙角处改造扩建成一个更大的绿地三角形花园AEF,要求EF过点C,若AB长15m,AD长10m.
如图,某住宅小区在围墙的墙角处有一矩形绿地ABCD,周围均为荒地,开发商欲把墙角处改造扩建成一个更大的绿地三角形花园AEF,要求EF过点C,若AB长15m,AD长10m.