��Ŀ����
��ͼ��ijסլС����Χǽ��ǽ�Ǵ���һ�����̵�ABCD����Χ��Ϊ�ĵأ�����������ǽ�Ǵ�����������һ��������̵������λ�AEF��Ҫ��EF����C����AB��15m��AD��10m��
��1��Ҫʹ�̵�AEF�����������400m2����AE�ij�Ӧ��ʲô��Χ�ڣ�
��2�����ڸ������������У�ԭ�̵ظ���ķ���Ϊÿƽ��100Ԫ���Աĵظ���ķ���Ϊÿƽ��200Ԫ����AE�ij����Ƕ���ʱ��������Ͷ��ķ�����С���������С���ã�
��1��Ҫʹ�̵�AEF�����������400m2����AE�ij�Ӧ��ʲô��Χ�ڣ�
��2�����ڸ������������У�ԭ�̵ظ���ķ���Ϊÿƽ��100Ԫ���Աĵظ���ķ���Ϊÿƽ��200Ԫ����AE�ij����Ƕ���ʱ��������Ͷ��ķ�����С���������С���ã�
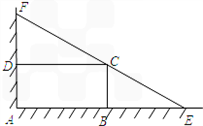
�⣺��1����BE=xm����DF= m
m
��AE=15+x��AF= +10
+10
���AEF�����Ϊ ��15+x����
��15+x���� +10��m2��
+10��m2��
���̵�AEF�����������400m2��
�� ��15+x����
��15+x���� +10����400
+10����400
��x2��50x+225��0
��5��x��15
��20��AE��30
��2�������⣬�ĵظ���������Сʱ��������Ͷ��ķ�����С����ʱ��AEF�������С����AEF�����Ϊ ��15+x����
��15+x���� +10��=
+10��= ��300�����ҽ���
��300�����ҽ��� ����x=15��AE=30mʱ��������Ͷ��ķ�����С����СΪ100��15��10+200����300��150��=45000Ԫ��
����x=15��AE=30mʱ��������Ͷ��ķ�����С����СΪ100��15��10+200����300��150��=45000Ԫ��
 m
m��AE=15+x��AF=
 +10
+10���AEF�����Ϊ
 ��15+x����
��15+x���� +10��m2��
+10��m2�����̵�AEF�����������400m2��
��
 ��15+x����
��15+x���� +10����400
+10����400��x2��50x+225��0
��5��x��15
��20��AE��30
��2�������⣬�ĵظ���������Сʱ��������Ͷ��ķ�����С����ʱ��AEF�������С����AEF�����Ϊ
 ��15+x����
��15+x���� +10��=
+10��= ��300�����ҽ���
��300�����ҽ��� ����x=15��AE=30mʱ��������Ͷ��ķ�����С����СΪ100��15��10+200����300��150��=45000Ԫ��
����x=15��AE=30mʱ��������Ͷ��ķ�����С����СΪ100��15��10+200����300��150��=45000Ԫ��
��ϰ��ϵ�д�
 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
�����Ŀ
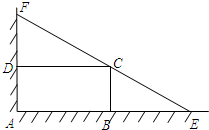 ��ͼ��ijסլС����Χǽ��ǽ�Ǵ���һ�����̵�ABCD����Χ��Ϊ�ĵأ�����������ǽ�Ǵ�����������һ��������̵������λ�AEF��Ҫ��EF����C����AB��15m��AD��10m��
��ͼ��ijסլС����Χǽ��ǽ�Ǵ���һ�����̵�ABCD����Χ��Ϊ�ĵأ�����������ǽ�Ǵ�����������һ��������̵������λ�AEF��Ҫ��EF����C����AB��15m��AD��10m��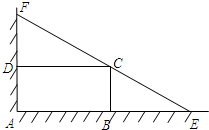 ��ͼ��ijסլС����Χǽ��ǽ�Ǵ���һ�����̵�ABCD����Χ��Ϊ�ĵأ�����������ǽ�Ǵ�����������һ��������̵������λ�AEF��Ҫ��EF����C����AB��15m��AD��10m��
��ͼ��ijסլС����Χǽ��ǽ�Ǵ���һ�����̵�ABCD����Χ��Ϊ�ĵأ�����������ǽ�Ǵ�����������һ��������̵������λ�AEF��Ҫ��EF����C����AB��15m��AD��10m��