题目内容
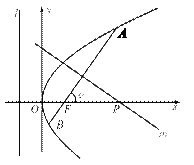
【题目】已知过点![]() 的动直线
的动直线![]() 与抛物线
与抛物线![]() :
: ![]() 相交于
相交于![]() ,
, ![]() 两点.当直线
两点.当直线![]() 的斜率是
的斜率是![]() 时,
时, ![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设线段![]() 的中垂线在
的中垂线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)设抛物线方程为![]() ,与直线
,与直线![]() 方程
方程![]() 联立,并设
联立,并设![]() ,结合韦达定理可
,结合韦达定理可![]() ,而已知条件
,而已知条件![]() 告诉我们有
告诉我们有![]() ,这样可解得
,这样可解得![]() ,得抛物线方程;
,得抛物线方程;
(2)设直线![]() 方程为
方程为![]() ,与抛物线方程联立方程组,同时设
,与抛物线方程联立方程组,同时设![]() 中点为
中点为![]() ,结合韦达定理可得
,结合韦达定理可得![]() ,从而得
,从而得![]() 中垂线方程,求出纵截距(关于
中垂线方程,求出纵截距(关于![]() 的函数),由直线与抛物线相交可得
的函数),由直线与抛物线相交可得![]() 的范围,从而可求得纵截距的范围.
的范围,从而可求得纵截距的范围.
试题解析:
(1)设![]() ,
, ![]() ,当直线
,当直线![]() 的斜率是
的斜率是![]() 时,
时, ![]() 的方程为
的方程为![]() ,
,
即![]() ,由
,由![]() 得:
得: ![]()
![]()
![]() ,
,
![]() ①,
①,![]() ②,
②,
又![]() ,
, ![]() ③,
③,
由①②③及![]() 得:
得: ![]() ,得抛物线
,得抛物线![]() 的方程为
的方程为![]() .
.
(2)设![]() :
: ![]() ,
, ![]() 的中点坐标为
的中点坐标为![]() ,
,
由 得
得![]() ④
④
![]() ,
, ![]() .
.
![]() 线段
线段![]() 的中垂线方程为
的中垂线方程为![]() ,
,
![]() 线段
线段![]() 的中垂线在
的中垂线在![]() 轴上的截距为:
轴上的截距为: ![]()
对于方程④,由![]() 得
得![]() 或
或![]() ,
, ![]() .
.

练习册系列答案
相关题目