题目内容
 有一个长方体容器ABCD-A1B1C1D1,装的水占恰好占其容积的一半;α表示水平的桌面,容器一边BC紧贴桌面,沿BC将其翻转使之略微倾斜,最后水面(阴影部分)与其各侧棱的交点分别是EFGH(如图),设翻转后容器中的水形成的几何体是M,翻转过程中水和容器接触面积为S,则下列说法正确的是
有一个长方体容器ABCD-A1B1C1D1,装的水占恰好占其容积的一半;α表示水平的桌面,容器一边BC紧贴桌面,沿BC将其翻转使之略微倾斜,最后水面(阴影部分)与其各侧棱的交点分别是EFGH(如图),设翻转后容器中的水形成的几何体是M,翻转过程中水和容器接触面积为S,则下列说法正确的是
- A.M是棱柱,S逐渐增大
- B.M是棱柱,S始终不变
- C.M是棱台,S逐渐增大
- D.M是棱台,S积始终不变
B
分析:由题意易得ABFE-DCGH为棱柱,进而可得S为定值.
解答:由面面平行的性质定理可知:EH∥FG.
由条件可知:EH∥AD,AD∥BC,
∴EH∥AD∥BC∥FG,又底面ABFE∥底面DCGH,
∴ABFE-DCGH为棱柱,
而在旋转的过程中,水和容器接触面积为
S=SAEHD+SBFGC= 为定值.
为定值.
故选B.
点评:本题考查命题真假的判断,理解和掌握棱柱的定义及面面平行的性质定理是解题的关键,属基础题.
分析:由题意易得ABFE-DCGH为棱柱,进而可得S为定值.
解答:由面面平行的性质定理可知:EH∥FG.
由条件可知:EH∥AD,AD∥BC,
∴EH∥AD∥BC∥FG,又底面ABFE∥底面DCGH,
∴ABFE-DCGH为棱柱,
而在旋转的过程中,水和容器接触面积为
S=SAEHD+SBFGC=
 为定值.
为定值.故选B.
点评:本题考查命题真假的判断,理解和掌握棱柱的定义及面面平行的性质定理是解题的关键,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有一个长方体容器ABCD-A1B1C1D1,装的水占恰好占其容积的一半;α表示水平的桌面,容器一边BC紧贴桌面,沿BC将其翻转使之略微倾斜,最后水面(阴影部分)与其各侧棱的交点分别是EFGH(如图),则下列对翻转后水形成的几何体形状说法正确的是( )
有一个长方体容器ABCD-A1B1C1D1,装的水占恰好占其容积的一半;α表示水平的桌面,容器一边BC紧贴桌面,沿BC将其翻转使之略微倾斜,最后水面(阴影部分)与其各侧棱的交点分别是EFGH(如图),则下列对翻转后水形成的几何体形状说法正确的是( )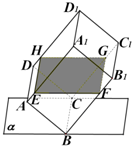 有一个长方体容器ABCD-A1B1C1D1,装的水占恰好占其容积的一半;α表示水平的桌面,容器一边BC紧贴桌面,沿BC将其翻转使之略微倾斜,最后水面(阴影部分)与其各侧棱的交点分别是EFGH(如图),设翻转后容器中的水形成的几何体是M,翻转过程中水和容器接触面积为S,则下列说法正确的是( )
有一个长方体容器ABCD-A1B1C1D1,装的水占恰好占其容积的一半;α表示水平的桌面,容器一边BC紧贴桌面,沿BC将其翻转使之略微倾斜,最后水面(阴影部分)与其各侧棱的交点分别是EFGH(如图),设翻转后容器中的水形成的几何体是M,翻转过程中水和容器接触面积为S,则下列说法正确的是( )

