题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率与双曲线
的离心率与双曲线![]() :
: ![]() 的离心率互为倒数,且经过点
的离心率互为倒数,且经过点![]() .
.
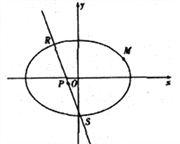
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,已知![]() 是椭圆上的两个点,线段
是椭圆上的两个点,线段![]() 的中垂线的斜率为
的中垂线的斜率为![]() 且与
且与![]() 交于点
交于点![]() ,
, ![]() 为坐标原点,求证:
为坐标原点,求证: ![]() 三点共线.
三点共线.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)由二者离心率互为倒数以及椭圆经过点![]() ,建立关于a,b,c的方程组从而得到椭圆的标准方程;(2)因为线段线段
,建立关于a,b,c的方程组从而得到椭圆的标准方程;(2)因为线段线段![]() 的中垂线的斜率为
的中垂线的斜率为![]() ,所以线段
,所以线段![]() 所在直线的斜率为
所在直线的斜率为![]() ,线段
,线段![]() 所在直线的方程为
所在直线的方程为![]() ,联立方程可得
,联立方程可得![]() ,利用韦达定理得到弦的中点的坐标,所以
,利用韦达定理得到弦的中点的坐标,所以![]() ,所以点
,所以点![]() 在定直线
在定直线![]() 上,而
上,而![]() 两点也在定直线
两点也在定直线![]() 上,所以
上,所以![]() 三点共线.
三点共线.
试题解析:
(1)因为双曲线![]() :
: ![]() 的离心率
的离心率![]() ,
,
而椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,所以椭圆
的离心率互为倒数,所以椭圆![]() 的离心率为
的离心率为![]() ,
,
设椭圆![]() 的半焦距为
的半焦距为![]() ,则
,则![]() .①
.①
又椭圆![]() 经过点
经过点![]() ,所以
,所以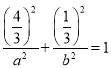 .②
.②
![]() ,③
,③
联立①②③,解得![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)因为线段线段![]() 的中垂线的斜率为
的中垂线的斜率为![]() ,所以线段
,所以线段![]() 所在直线的斜率为
所在直线的斜率为![]() .
.
所以可设线段![]() 所在直线的方程为
所在直线的方程为![]() ,
,
设点![]() ,
,
联立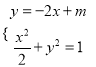 ,消去
,消去![]() ,并整理得
,并整理得![]() ,
,
显然![]() .
.
所以![]()
![]() ,
,
则![]()
因为![]() ,所以
,所以![]() ,
,
所以点![]() 在定直线
在定直线![]() 上,而
上,而![]() 两点也在定直线
两点也在定直线![]() 上,所以
上,所以![]() 三点共线.
三点共线.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目