题目内容
解不等式: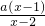 >1 (a<1).
>1 (a<1).
解:原不等式可化为 ,
,
即[(a-1)x+(2-a)](x-2)>0.
∵a<1,∵(x-2)(x- )<0
)<0
当 >2时,即0<a<1时,解集为{x|2<x<
>2时,即0<a<1时,解集为{x|2<x< };
};
当 =2时,即a=0时,解集为φ;
=2时,即a=0时,解集为φ;
当 <2时,即a<0时,解集为{x|
<2时,即a<0时,解集为{x| <x<2}.
<x<2}.
综上,当a<0时,原不等式的解集为{x| <x<2},
<x<2},
当a=0时,原不等式的解集为空集,
当0<a<1时,原不等式的解集为{x|2<x< }.
}.
分析:把原不等式的右边的1移项到左边,通分后可将除的形式化为积的形式,因为a小于1,所以a-1小于0,在不等式两边都除以a-1,不等号的方向改变,然后分三种情况:① 大于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集;②当
大于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集;②当 等于2,解出a的值,把a的值代入求得到原不等式无解;③当
等于2,解出a的值,把a的值代入求得到原不等式无解;③当 小于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集.
小于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集.
点评:此题考查了其他不等式的解法,以及运用分类讨论的思想解决数学问题,是一道综合题.
 ,
,即[(a-1)x+(2-a)](x-2)>0.
∵a<1,∵(x-2)(x-
 )<0
)<0当
 >2时,即0<a<1时,解集为{x|2<x<
>2时,即0<a<1时,解集为{x|2<x< };
};当
 =2时,即a=0时,解集为φ;
=2时,即a=0时,解集为φ;当
 <2时,即a<0时,解集为{x|
<2时,即a<0时,解集为{x| <x<2}.
<x<2}.综上,当a<0时,原不等式的解集为{x|
 <x<2},
<x<2},当a=0时,原不等式的解集为空集,
当0<a<1时,原不等式的解集为{x|2<x<
 }.
}.分析:把原不等式的右边的1移项到左边,通分后可将除的形式化为积的形式,因为a小于1,所以a-1小于0,在不等式两边都除以a-1,不等号的方向改变,然后分三种情况:①
 大于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集;②当
大于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集;②当 等于2,解出a的值,把a的值代入求得到原不等式无解;③当
等于2,解出a的值,把a的值代入求得到原不等式无解;③当 小于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集.
小于2,列出关于a的不等式,求出不等式的解集即可得到a的范围,当a取这个范围的值时,求出不等式的解集.点评:此题考查了其他不等式的解法,以及运用分类讨论的思想解决数学问题,是一道综合题.

练习册系列答案
相关题目
 >1 (a<1).
>1 (a<1).