题目内容
设x∈z,则f(x)=cos
x的值域是( )
| π |
| 3 |
分析:由于x∈z,先求出f(x)=cos
x的周期为 6,求出f(0)、f(1)、f(2)、f(2)、f(3)、f(4)、
f(5)的值,即可得到f(x)=cos
x的值域.
| π |
| 3 |
f(5)的值,即可得到f(x)=cos
| π |
| 3 |
解答:解:∵x∈z,f(x)=cos
x的周期为
=6,
f(0)=cos0=1,f(1)=cos
=
,f(2)=cos
=-
,
f(3)=cosπ=-1,f(4)=cos
=-
,f(5)=cos
=cos(-
)=
,
则f(x)=cos
x的值域是 {-1,-
,
,1}.
故选B.
| π |
| 3 |
| 2π | ||
|
f(0)=cos0=1,f(1)=cos
| π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
f(3)=cosπ=-1,f(4)=cos
| 4π |
| 3 |
| 1 |
| 2 |
| 5π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
则f(x)=cos
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题主要考查余弦函数的定义域和值域,余弦函数的周期性的应用,属于基础题.

练习册系列答案
相关题目
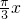 的值域是
的值域是 }
} 的值域是( )
的值域是( ) }
} ,
, ,1}
,1} ,0,
,0, ,1}
,1} ,1}
,1}