题目内容
 如图1所示,在边长为
如图1所示,在边长为![]() 的正方形
的正方形![]() 中,
中,![]()
![]() ,且
,且![]() ,
,![]() ,
,![]() 分别交
分别交![]()
![]() 于点
于点![]() ,将该正方形沿
,将该正方形沿![]() 、
、![]() 折叠,使得
折叠,使得![]() 与
与![]() 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱![]() 中
中
(Ⅰ)求证:![]()
![]() ;
;
(Ⅱ)在底边![]() 上有一点
上有一点![]() ,
,![]() ,
,
求证:![]() 面
面![]()
(III)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅰ)略,(Ⅱ)略,(Ⅲ)直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
解析:
(Ⅰ)证明:因为![]() ,
,![]() ,
,
所以![]() ,从而
,从而![]() ,即
,即![]() .………………………2分
.………………………2分
又因为![]() ,而
,而![]() ,
,
所以![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]()
所以![]()
![]() ;………………4分
;………………4分
(Ⅱ)解:过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
因为![]()
![]()
![]()
![]() ……………6分
……………6分
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]() ,所以
,所以![]() 平面
平面![]() …………………………8分
…………………………8分
(III)解:由图1知,![]() ,分别以
,分别以![]() 为
为![]() 轴,
轴,
则![]()
![]() ………10分
………10分
设平面![]() 的法向量为
的法向量为![]() ,
,
所以 得
得![]() ,
,
令![]() ,则
,则![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() …………………………12分
…………………………12分

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
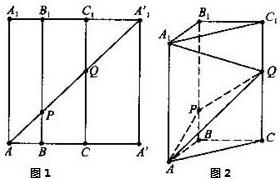 如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题:
如图1所示,在边长为12的正方形AA′A′1A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA′1分别交BB1,CC1于点P、Q,将该正方形沿BB1、CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,请在图2中解决下列问题: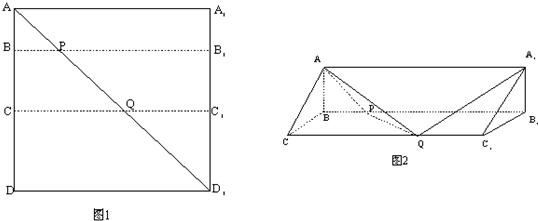
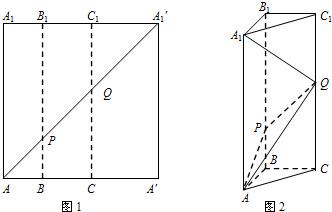 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.