题目内容
已知函数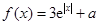 (
(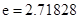 是自然对数的底数)的最小值为
是自然对数的底数)的最小值为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)已知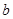
 且
且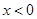 ,试解关于
,试解关于 的不等式
的不等式 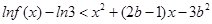 ;
;
(Ⅲ)已知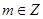 且
且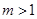 .若存在实数
.若存在实数 ,使得对任意的
,使得对任意的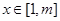 ,都有
,都有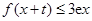 ,试求
,试求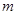 的最大值.
的最大值.
(1)
(2)当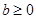 时,不等式的解为
时,不等式的解为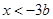 ;当
;当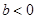 时,不等式的解为
时,不等式的解为
(3)3
解析试题分析:解:(Ⅰ)因为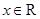 ,所以
,所以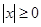 ,故
,故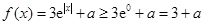 ,
,
因为函数 的最小值为
的最小值为 ,所以
,所以 . 3分
. 3分
(Ⅱ)由(Ⅰ)得,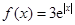 .
.
当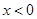 时,
时,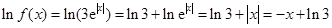 , 5分
, 5分
故不等式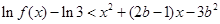 可化为:
可化为: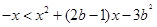 ,
,
即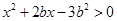 , 6分
, 6分
得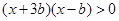 ,
,
所以,当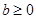 时,不等式的解为
时,不等式的解为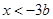 ;
;
当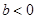 时,不等式的解为
时,不等式的解为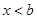 . 8分
. 8分
(Ⅲ)∵当 且
且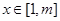 时,
时,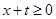 ,
,
∴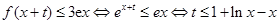 .
.
∴原命题等价转化为:存在实数 ,使得不等式
,使得不等式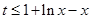 对任意
对任意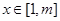 恒成立. 10分
恒成立. 10分
令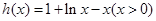 .
.
∵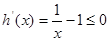 ,∴函数
,∴函数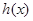 在
在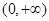 为减函数. 11分
为减函数. 11分
又∵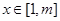 ,∴
,∴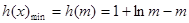 . 12分
. 12分
∴要使得对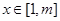 ,
,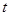 值恒存在,只须
值恒存在,只须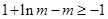 . 13分
. 13分
∵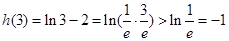 ,
,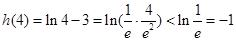
且函数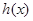 在
在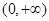 为减函数,
为减函数,
∴满足条件的最大整数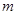 的值为3. 14分
的值为3. 14分
考点:函数与不等式
点评:主要是考查了函数与不等式的综合运用,以及导数研究函数单调性的求解属于中档题。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为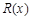 万元,且
万元,且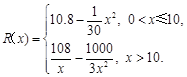
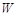 (万元)关于年产量
(万元)关于年产量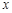 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为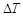 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量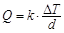 ,其中
,其中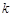 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为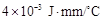 ,空气的热传导系数为
,空气的热传导系数为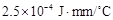 .)
.)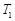 ,
,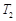 ,内层玻璃外侧温度为
,内层玻璃外侧温度为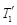 ,外层玻璃内侧温度为
,外层玻璃内侧温度为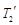 ,且
,且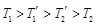 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
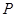 :函数
:函数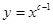 在
在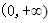 上为减函数, 命题
上为减函数, 命题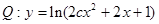 的值域为
的值域为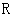 ,命题
,命题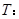 函数
函数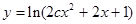 定义域为
定义域为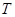 为真命题,求
为真命题,求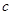 的取值范围。
的取值范围。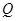 为真命题,
为真命题,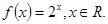
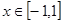 ,使得
,使得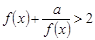 成立,求实数
成立,求实数 的取值范围;
的取值范围;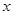 的不等式
的不等式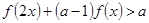 ;
; ,求
,求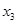 的最大值.
的最大值. 
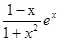 .
.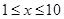 ),每小时可获得利润是
),每小时可获得利润是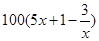 元.
元. ,高为2
,高为2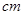 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?