题目内容
(本题满分16分)已知函数 在
在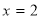 处的切线
处的切线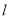 与直线
与直线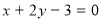 平行.
平行.
(1)求实数 的值;
的值;
(2)若关于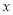 的方程
的方程 在
在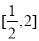 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)记函数 ,设
,设 是函数
是函数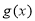 的两个极值点,若
的两个极值点,若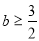 ,且
,且 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
(1)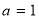 (2)
(2)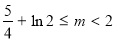 (3)
(3)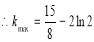
【解析】
试题分析:(1)由题知斜率为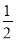 ,所以函数在
,所以函数在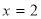 处的导数为
处的导数为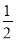 ,列出方程,解出
,列出方程,解出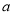
(2)构造函数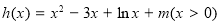 ,将有两个不相等的实根转化为函数有两上零点;然后求导,列表,根据图像列出不等式
,将有两个不相等的实根转化为函数有两上零点;然后求导,列表,根据图像列出不等式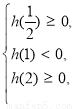 (3)由
(3)由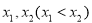 是函数
是函数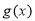 的两个极值点,求导得
的两个极值点,求导得
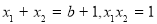 ,根据
,根据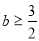 ,求出
,求出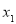 或
或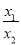 的范围;要求
的范围;要求 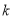 的最大值,即求
的最大值,即求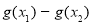 的最小值,根据
的最小值,根据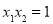 ,构造关于
,构造关于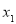 的函数,或直接构造关于
的函数,或直接构造关于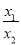 的函数, 求出最值。
的函数, 求出最值。
试题解析:【解析】
(1)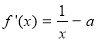 2分
2分
∵函数在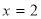 处的切线
处的切线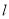 与直线
与直线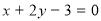 平行 ∴
平行 ∴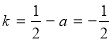 ,
,
解得: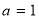 ; 4分
; 4分
(2)由(1)得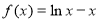 ,∴
,∴ ,即
,即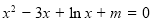
设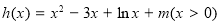 ,
,
则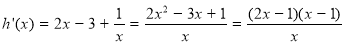
令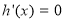 ,得
,得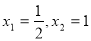 , 列表得:
, 列表得:
|
|
| 1 | (1,2) | 2 |
| 0 | - | 0 | + | |
| 极大值 |
| 极小值 |
|
|
∴当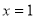 时,
时,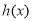 的极小值为
的极小值为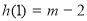 ,
,
又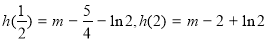 7分
7分
∵方程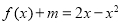 在
在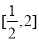 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
∴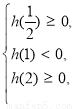 即
即 解得:
解得: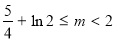 ;
;
(也可分离变量解) 10分
(3)解法(一)
∵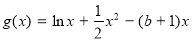 ,∴
,∴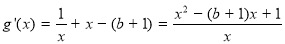
∴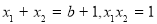 ,
,
∴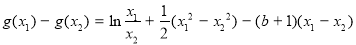
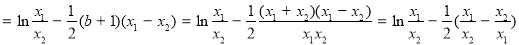
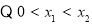 设
设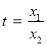 ,则
,则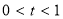 ,令
,令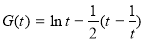 ,
,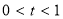
则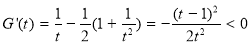 ,∴
,∴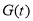 在
在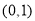 上单调递减; 12分
上单调递减; 12分
∵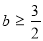 ,∴
,∴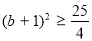
∵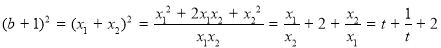
∴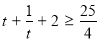 ∴
∴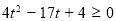 ∴
∴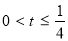 14分
14分
∴当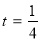 时,
时,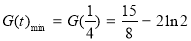 ∴
∴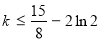
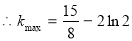 . 16分
. 16分
解法(二)
∵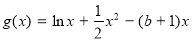 ,∴
,∴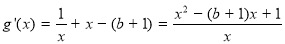
∴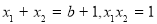 , ∴
, ∴ 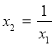 ∵
∵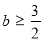 ∴
∴ 
解得: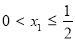 12分
12分
∴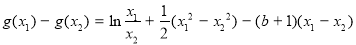
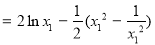
设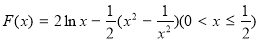 ,则
,则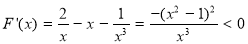
∴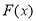 在
在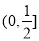 上单调递减; 14分
上单调递减; 14分
∴当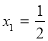 时,
时,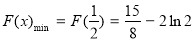 ∴
∴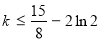
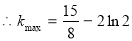 . 16分
. 16分
考点:导数的几何意义,导数与不等式









 ,则目标函数
,则目标函数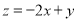 的最大值是( )
的最大值是( )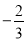
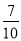 为概率的事件是
为概率的事件是 中,
中,  ,则
,则 = .
= .  中,侧面
中,侧面 是菱形,
是菱形, 与
与 交于点
交于点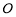 ,E是AB的中点.
,E是AB的中点.
 平面
平面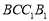 ;
; ,求证:
,求证: .
.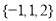 中随机选取一个数记为
中随机选取一个数记为 ,从集合
,从集合 中随机选取一个数记为
中随机选取一个数记为 ,则方程
,则方程 表示双曲线的概率为
表示双曲线的概率为  满足
满足 ,若离心率为
,若离心率为 ,则
,则 的最小值为_______.
的最小值为_______.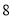 的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,则两个正方形的边长各是 ; ;
的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,则两个正方形的边长各是 ; ;