题目内容
将函数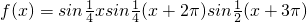 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=2nan,数列{bn}的前n项和为Tn,求Tn的表达式.
解:(1)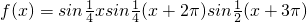
=

=
=
根据正弦函数的性质,
其极值点为 ,
,
它在(0,+∞)内的全部极值点构成以 为首项,π为公差的等差数列,
为首项,π为公差的等差数列,
数列{an}的通项公式为
 .
.
(2)由(1)得出
∴ ,两边乘以2得,
,两边乘以2得,

两式相减,得
=
=
=-π[(2n-3)•2n+3]
∴Tn=π[(2n-3)•2n+3]
分析:(1)利用诱导公式将f(x)化简得出f(x)= ,根据正弦函数的性质,其极值点为
,根据正弦函数的性质,其极值点为 ,它在(0,+∞)内的全部极值点构成以
,它在(0,+∞)内的全部极值点构成以 为首项,π为公差的等差数列.通项公式可求.
为首项,π为公差的等差数列.通项公式可求.
(2)由(1)得出 ,利用错位相消法计算即可.
,利用错位相消法计算即可.
点评:本题考查了三角函数式的恒等变形、三角函数的性质,等差数列通项公式求解,以及数列求和中的错位相消法.
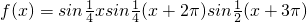
=


=

=

根据正弦函数的性质,
其极值点为
 ,
,它在(0,+∞)内的全部极值点构成以
 为首项,π为公差的等差数列,
为首项,π为公差的等差数列,数列{an}的通项公式为
 .
.(2)由(1)得出

∴
 ,两边乘以2得,
,两边乘以2得,
两式相减,得

=

=

=-π[(2n-3)•2n+3]
∴Tn=π[(2n-3)•2n+3]
分析:(1)利用诱导公式将f(x)化简得出f(x)=
 ,根据正弦函数的性质,其极值点为
,根据正弦函数的性质,其极值点为 ,它在(0,+∞)内的全部极值点构成以
,它在(0,+∞)内的全部极值点构成以 为首项,π为公差的等差数列.通项公式可求.
为首项,π为公差的等差数列.通项公式可求.(2)由(1)得出
 ,利用错位相消法计算即可.
,利用错位相消法计算即可.点评:本题考查了三角函数式的恒等变形、三角函数的性质,等差数列通项公式求解,以及数列求和中的错位相消法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
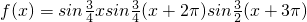 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an},(n=1,2,3,…).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an},(n=1,2,3,…).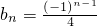 ,(n=1,2,3,…).
,(n=1,2,3,…).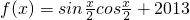 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).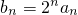 ,数列{bn}的前n项和为Tn,求Tn的表达式.
,数列{bn}的前n项和为Tn,求Tn的表达式. 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*). 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}.
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}.