题目内容
将函数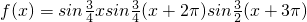 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an},(n=1,2,3,…).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an},(n=1,2,3,…).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=sinansinan+1sinan+2,求证: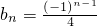 ,(n=1,2,3,…).
,(n=1,2,3,…).
解:(Ⅰ)∵
=
∴f(x)的极值点为 ,
,
从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,
∴ ,(n=1,2,3,…)
,(n=1,2,3,…)
(Ⅱ)由 知对任意正整数n,
知对任意正整数n,
an都不是π的整数倍,
所以sinan≠0,
从而bn=sinansinan+1sinan+2≠0
于是
又 ,
,
{bn}是以 为首项,-1为公比的等比数列.
为首项,-1为公比的等比数列.
∴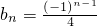 ,(n=1,2,3,…)
,(n=1,2,3,…)
分析:(Ⅰ)由 =-
=- ,知f(x)的极值点为
,知f(x)的极值点为 ,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以
,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以 为首项,
为首项, 为公差的等差数列,由此能求出数列{an}的通项公式.
为公差的等差数列,由此能求出数列{an}的通项公式.
(Ⅱ)由 知对任意正整数n,an都不是π的整数倍,知sinan≠0,从而bn=sinansinan+1sinan+2≠0.于是
知对任意正整数n,an都不是π的整数倍,知sinan≠0,从而bn=sinansinan+1sinan+2≠0.于是 ,由此能够证明
,由此能够证明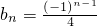 ,(n=1,2,3,…).
,(n=1,2,3,…).
点评:第(Ⅰ)题考查数列的通项公式的求法,解题时要认真审题,注意三角函数的性质和应用,合理运用三角函数的极值点进行解题.
第(Ⅱ)求证: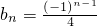 ,(n=1,2,3,…).解题时要认真审题,利用三角函数的性质证明{bn}是以
,(n=1,2,3,…).解题时要认真审题,利用三角函数的性质证明{bn}是以 为首项,-1为公比的等比数列.
为首项,-1为公比的等比数列.

=

∴f(x)的极值点为
 ,
,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以
 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,∴
 ,(n=1,2,3,…)
,(n=1,2,3,…)(Ⅱ)由
 知对任意正整数n,
知对任意正整数n,an都不是π的整数倍,
所以sinan≠0,
从而bn=sinansinan+1sinan+2≠0
于是

又
 ,
,{bn}是以
 为首项,-1为公比的等比数列.
为首项,-1为公比的等比数列.∴
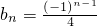 ,(n=1,2,3,…)
,(n=1,2,3,…)分析:(Ⅰ)由
 =-
=- ,知f(x)的极值点为
,知f(x)的极值点为 ,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以
,从而它在区间(0,+∞)内的全部极值点按从小到大排列构成以 为首项,
为首项, 为公差的等差数列,由此能求出数列{an}的通项公式.
为公差的等差数列,由此能求出数列{an}的通项公式.(Ⅱ)由
 知对任意正整数n,an都不是π的整数倍,知sinan≠0,从而bn=sinansinan+1sinan+2≠0.于是
知对任意正整数n,an都不是π的整数倍,知sinan≠0,从而bn=sinansinan+1sinan+2≠0.于是 ,由此能够证明
,由此能够证明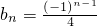 ,(n=1,2,3,…).
,(n=1,2,3,…).点评:第(Ⅰ)题考查数列的通项公式的求法,解题时要认真审题,注意三角函数的性质和应用,合理运用三角函数的极值点进行解题.
第(Ⅱ)求证:
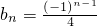 ,(n=1,2,3,…).解题时要认真审题,利用三角函数的性质证明{bn}是以
,(n=1,2,3,…).解题时要认真审题,利用三角函数的性质证明{bn}是以 为首项,-1为公比的等比数列.
为首项,-1为公比的等比数列. 
练习册系列答案
相关题目
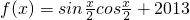 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).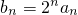 ,数列{bn}的前n项和为Tn,求Tn的表达式.
,数列{bn}的前n项和为Tn,求Tn的表达式.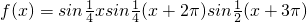 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*). 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*).
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}(n∈N*). 在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}.
在区间(0,+∞)内的全部极值点按从小到大的顺序排成数列{an}.