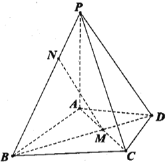
题目内容
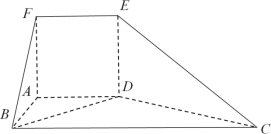
【题目】如图，ABCD为矩形，点A、E、B、F共面，且
和
均为等腰直角三角形，且
90°．
（Ⅰ）若平面ABCD
平面AEBF，证明平面BCF平面ADF；
（Ⅱ）问在线段EC上是否存在一点G，使得BG∥平面CDF，若存在，求出此时三棱锥G-ABE与三棱锥G-ADF的体积之比．
【答案】（Ⅰ）见证明；（Ⅱ）见解析
【解析】
（Ⅰ）根据
为矩形，结合面面垂直性质定理可得
平面
，即
，结合
，即可得
平面
，最后根据面面垂直判定定理可得结果；（Ⅱ）首先易得
平面
，再证
平面，进而面面平行，延长
到点
，使得
，可得
是平行四边形，过点
作
的平行线，交
于点
，此
即为所求，通过
可得结果.
（Ⅰ）∵ABCD为矩形，∴BC⊥AB，
又∵平面ABCD⊥平面AEBF，BC
平面ABCD，平面ABCD∩平面AEBF=AB，
∴BC⊥平面AEBF，
又∵AF平面AEBF，∴BC⊥AF.
∵∠AFB=90°，即AF⊥BF，且BC、BF平面BCF，BC∩BF=B，
∴AF⊥平面BCF
又∵AF平面ADF，∴平面ADF
平面BCF.
（2）∵BC∥AD，AD平面ADF，∴BC∥平面ADF.
∵
和
均为等腰直角三角形，且
90°，
∴∠FAB=∠ABE=45°，∴AF∥BE，又AF平面ADF，∴BE∥平面ADF，
∵BC∩BE=B，∴平面BCE∥平面ADF.
延长EB到点H，使得BH =AF，又BC 
AD，连CH、HF，易证ABHF是平行四边形，
∴HFABCD，∴HFDC是平行四边形，∴CH∥DF.
过点B作CH的平行线，交EC于点G，即BG∥CH∥DF，（DF平面CDF）
∴BG∥平面CDF，即此点G为所求的G点.
又BE=
，∴EG=
，又
，
，
故
..
练习册系列答案
名题金卷系列答案
相关题目
