题目内容
15.若?x∈D,g(x)≤f(x)≤h(x),则称函数f(x)为函数g(x)到函数h(x)在区间D上的“随性函数”.已知函数f(x)=kx,g(x)=x2-2x,h(x)=(x+1)(lnx+1),且f(x)是g(x)到h(x)在区间[1,e]上的“随性函数”,则实数k的取值范围是[e-2,2].分析 问题转化为k≥x-2,x∈[1,e],即k≥e-2在x∈[1,e]恒成立以及k≤$\frac{(x+1)(lnx+1)}{x}$在[1,e]恒成立,令m(x)=$\frac{(x+1)(lnx+1)}{x}$,x∈[1,e],根据函数的单调性求出m(x)的最小值,从而求出k的范围即可.
解答 解:由题意得:kx≥x2-2x在x∈[1,e]恒成立,即k≥x-2,
而x∈[1,e],故k≥e-2,
由kx≤(x+1)(lnx+1)在x∈[1,e]恒成立,
得k≤$\frac{(x+1)(lnx+1)}{x}$在[1,e]恒成立,
令m(x)=$\frac{(x+1)(lnx+1)}{x}$,x∈[1,e],
则m′(x)=$\frac{x-lnx}{{x}^{2}}$>0,
m(x)在[1,e]递增,
故m(x)min=m(1)=2,
故k≤2,
综上,k∈[e-2,2],
故答案为:[e-2,2].
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若某商品销售量y(件)与销售价格x(元/件)负相关,则其回归直线方程可能是( )
| A. | $\stackrel{∧}{y}$=-10x-100 | B. | $\stackrel{∧}{y}$=10x-100 | C. | $\stackrel{∧}{y}$=-10x+200 | D. | $\stackrel{∧}{y}$=10x-200 |
3.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积是( )
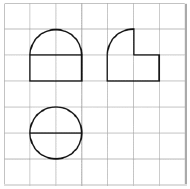

| A. | $\frac{7π}{2}$ | B. | 4π | C. | $\frac{9π}{2}$ | D. | 5π |
10.执行如图所示的程序框图,输出的S值为( )


| A. | 4 | B. | 8 | C. | 14 | D. | 18 |
7.下列函数中,周期为1的奇函数是( )
| A. | y=cos2πx | B. | y=sinπxcosπx | C. | $y=tan\frac{π}{2}x$ | D. | $y=sin(2πx+\frac{π}{3})$ |
4.已知x∈R,则“|x-3|-|x-1|<2”是“x>3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知离心率为e的双曲线$\frac{x^2}{a^2}-\frac{y^2}{7}=1$,其与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点重合,则e的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4\sqrt{23}}{23}$ | C. | $\frac{4}{3}$ | D. | $\frac{\sqrt{23}}{4}$ |