题目内容
若圆C的圆心坐标为（2，-3），且圆C经过点M（5，-7），求其标准方程并判断点P（2，4）与圆的关系．
分析：根据题意，可设所求圆的方程，利用该圆过点M（5，-7），可求得r2，从而可得这个圆的标准方程，然后判断点与圆的位置关系即可．
解答：解：依题意可设所求圆的方程为（x-2）2+（y+3）2=r2．
∵点M（5，-7）在圆上，∴r2=（5-2）2+（-7+3）2=25
∴圆的标准方程是（x-2）2+（y+3）2=52．
点P（2，4）代入圆的方程可得：（2-2）2+（4+3）2=49＞25．
所以点在圆外．
∵点M（5，-7）在圆上，∴r2=（5-2）2+（-7+3）2=25
∴圆的标准方程是（x-2）2+（y+3）2=52．
点P（2，4）代入圆的方程可得：（2-2）2+（4+3）2=49＞25．
所以点在圆外．
点评：本题考查圆的标准方程，设出圆的标准方程后，求其半径是关键，判断点与圆的位置关系看点的坐标是否满足方程．
练习册系列答案
中考解读考点精练系列答案
相关题目
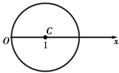如图，在极坐标系中，圆C的圆心坐标为（1，0），半径为1．