题目内容
过点P(2,1)的直线y-1=k(x-2)(k为常数,k≠ )分别交两坐标轴于A、B两点,若
)分别交两坐标轴于A、B两点,若 =t
=t +s
+s ,O为坐标原点,则
,O为坐标原点,则 +
+ 的最小值是
的最小值是
- A.4
- B.3
- C.2
- D.1
A
分析:根据题意,点P在直线AB上且在A、B两点之间,所以可设 ,其中λ>0.由此推导出
,其中λ>0.由此推导出  =
=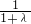
 +
+
 ,再结合已知等式:
,再结合已知等式: =t
=t  +s
+s  ,得到
,得到  ,
, ,从而得到t+s=1且t、s都是小于1的正数.最后利用“1的代换”和基本不等式,可以求出
,从而得到t+s=1且t、s都是小于1的正数.最后利用“1的代换”和基本不等式,可以求出  +
+ 的最小值.
的最小值.
解答:∵点P在线段AB上,即在直线AB上且在A、B两点之间,
∴可以设 且λ>0,
且λ>0,
∵ 、
、 ,
,
∴ ,
,
∴ =
=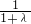
 +
+
 ,
,
再结合题意: =t
=t  +s
+s  ,得到
,得到  .
.
∴t+s=1,因为λ>0所以t、s都是小于1的正数,
∴ +
+ =(t+s)(
=(t+s)(  +
+ )=2+(
)=2+(  ),
),
∵ ,
,
∴ +
+ ≥4,当且仅当t=s=
≥4,当且仅当t=s= 时,
时, +
+ 的最小值为4.
的最小值为4.
故选A.
点评:本题考查了平面向量基本定理和基本不等式求最值等知识点,属于中档题.解题过程中巧妙地避免了运用坐标进行繁琐的代数化简,请同学们注意这点.
分析:根据题意,点P在直线AB上且在A、B两点之间,所以可设
 ,其中λ>0.由此推导出
,其中λ>0.由此推导出  =
=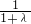
 +
+
 ,再结合已知等式:
,再结合已知等式: =t
=t  +s
+s  ,得到
,得到  ,
, ,从而得到t+s=1且t、s都是小于1的正数.最后利用“1的代换”和基本不等式,可以求出
,从而得到t+s=1且t、s都是小于1的正数.最后利用“1的代换”和基本不等式,可以求出  +
+ 的最小值.
的最小值.解答:∵点P在线段AB上,即在直线AB上且在A、B两点之间,
∴可以设
 且λ>0,
且λ>0,∵
 、
、 ,
,∴
 ,
,∴
 =
=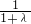
 +
+
 ,
,再结合题意:
 =t
=t  +s
+s  ,得到
,得到  .
.∴t+s=1,因为λ>0所以t、s都是小于1的正数,
∴
 +
+ =(t+s)(
=(t+s)(  +
+ )=2+(
)=2+(  ),
),∵
 ,
,∴
 +
+ ≥4,当且仅当t=s=
≥4,当且仅当t=s= 时,
时, +
+ 的最小值为4.
的最小值为4.故选A.
点评:本题考查了平面向量基本定理和基本不等式求最值等知识点,属于中档题.解题过程中巧妙地避免了运用坐标进行繁琐的代数化简,请同学们注意这点.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

 椭圆E:
椭圆E: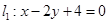 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
.