题目内容
(本小题满分12分)如图, 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC="BC=" AA1=1,AB=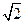 点D是AB的中点,
点D是AB的中点,
求证:(1)AC 1//平面CDB1; ( 2 )BC1⊥平面AB1C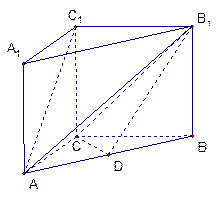
 点D是AB的中点,
点D是AB的中点,求证:(1)AC 1//平面CDB1; ( 2 )BC1⊥平面AB1C

证明:(1)设BC1与B1C设相交于O,连接OD
则O是BC1中点
在△ABC1中,OD中位线,OD// AC 1
因为
所以AC 1//平面CDB1………………………5分
(2)由于 平面
平面 ,
, 平面
平面 所以
所以
因为 ,所以
,所以
又因为 ,
,
所以
所以
在矩形 中,
中, ,从而
,从而
因为 ,
,
所以 ………………………………………………………………12分
………………………………………………………………12分
则O是BC1中点
在△ABC1中,OD中位线,OD// AC 1
因为

所以AC 1//平面CDB1………………………5分
(2)由于
 平面
平面 ,
, 平面
平面 所以
所以
因为
 ,所以
,所以
又因为
 ,
,
所以

所以

在矩形
 中,
中, ,从而
,从而
因为
 ,
,
所以
 ………………………………………………………………12分
………………………………………………………………12分略

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
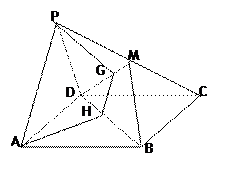

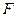 为
为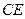 上的点,且
上的点,且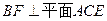 ,
,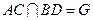 .
.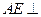 平面
平面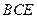 ;
;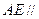 平面
平面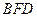 ;
;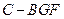 的体积
的体积 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题中正确的是( )
是两个不同的平面,则下列命题中正确的是( )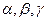 是三个不重合的平面,l 是直线,给出下列四个命题:
是三个不重合的平面,l 是直线,给出下列四个命题: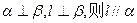 ;
; 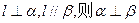 ;
;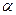 的距离相等,则l//
的距离相等,则l//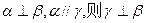 .
.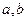 为不重合的两条直线,
为不重合的两条直线,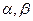 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题: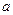 ∥
∥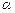 且
且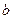 ∥
∥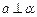 且
且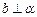 ,则
,则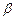 ,则
,则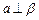 ,则
,则 ,下列命题正确的是
,下列命题正确的是


