题目内容
10.已知y=f(x)为定义在R上的奇函数.(1)若y=f(x)在(0,+∞)上为减函数,判断(-∞,0)上的单调性并证明;
(2)若x>0时,f(x)=x2+sinx+1,求f(x)的解析式.
分析 (1)利用作差法.我们可以任取区间上满足-∞<x1<x2<0的两个实数,再根据函数f(x)是奇函数,且在(0,+∞)上是减函数,易判断函数f(x)在(-∞,0)上的单调性.
(2)先求f(0)=0,再设x<0,由奇函数的性质f(x)=-f(-x),利用x>0时的表达式求出x<0时函数的表达式.
解答 解:(1)任取x1,x2∈(-∞,0),且-∞<x1<x2<0
则0<-x2<-x1≤+∞
又∵f(x)在(0,+∞)上是减函数,
∴f(-x2)>f(-x1)
又∵f(x)是奇函数,
∴f(-x2)=-f(x2),f(-x1)=-f(x1)
∴f(x2)<f(x1),即f(x)在(-∞,0)上单调递减.
(2)∵函数f(x)是定义在R上的奇函数,
∴f(0)=0,且f(-x)=-f(x),
∴f(x)=-f(-x),
设x<0,则-x>0,
∴f(-x)=x2-sinx+1,
∴f(x)=-f(-x)=-x2+sinx-1,
∴f(x)=$\left\{\begin{array}{l}{{x}^{2}+sinx+1,x>0}\\{0,x=0}\\{-{x}^{2}+sinx-1,x<0}\end{array}\right.$.
点评 本题考查的知识点是函数的奇偶性与单调性的综合,考查奇函数的性质求解函数的解析式,关键是利用原点两侧的函数表达式之间的关系解题,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
20.如图,直线AB∥CD∥EF,若AC=3,CE=4,则$\frac{BD}{BF}$的值是( )
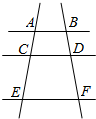

| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
1.设函数f(x)=$\frac{2}{5}$(ex+e-x),则f(x)是( )
| A. | 奇函数 | B. | 非奇非偶函数 | ||
| C. | 偶函数 | D. | 既是奇函数又是偶函数 |
18.已知M(x1,y1),N(x2,y2)是双曲线线$\frac{{x}^{2}}{2}$-y2=1上的两个动点,且x1+x2=1,若线段MN的垂直平分线过定点Q,则Q点的坐标为( )
| A. | ($\frac{1}{2}$,0) | B. | ($\frac{3}{4}$,1) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{3}{4}$,0) |
 如图,四面体ABCD中,O、E分别BD、BC的中点,CA=CB=CD=BD=2AO=2,AB=AD.
如图,四面体ABCD中,O、E分别BD、BC的中点,CA=CB=CD=BD=2AO=2,AB=AD.