题目内容
已知函数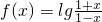 .
.
(1)判断并证明f(x)的奇偶性;
(2)求证: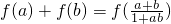 ;
;
(3)已知a,b∈(-1,1),且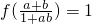 ,
,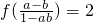 ,求f(a),f(b)的值.
,求f(a),f(b)的值.
解:(1)由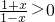 可得函数的定义域(-1,1),关于原点对称
可得函数的定义域(-1,1),关于原点对称
∵ =
= 故函数f(x)为奇函数
故函数f(x)为奇函数
(2)∵f(a)+f(b)= =
=
 =
= =
=
∴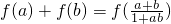
(3)∵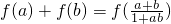 =1
=1
∴f(a)+f(b)=1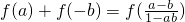 =2
=2
∴f(a)+f(-b)=2
∵f(-b)=-f(b),
∴f(a)-f(b)=2,解得: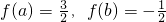
分析:(1)由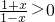 可得函数的定义域(-1,1),关于原点对称,再由
可得函数的定义域(-1,1),关于原点对称,再由 =
= 可判断函数奇偶性
可判断函数奇偶性
(2)分别计算 f(a)+f(b)与 可证
可证
(3)由(2)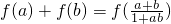 可得f(a)+f(b)=1
可得f(a)+f(b)=1 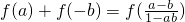 ,f(a)+f(b)=2结合奇函数的性质可得f(-b)=-f(b),从而可求
,f(a)+f(b)=2结合奇函数的性质可得f(-b)=-f(b),从而可求
点评:本题主要考查了对数函数的定义域的求解,函数的奇欧性的判断及利用对数的基本运算性质证明等式,属于对数知识的综合应用.
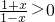 可得函数的定义域(-1,1),关于原点对称
可得函数的定义域(-1,1),关于原点对称∵
 =
= 故函数f(x)为奇函数
故函数f(x)为奇函数(2)∵f(a)+f(b)=
 =
=
 =
= =
=
∴
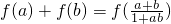
(3)∵
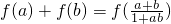 =1
=1∴f(a)+f(b)=1
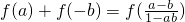 =2
=2∴f(a)+f(-b)=2
∵f(-b)=-f(b),
∴f(a)-f(b)=2,解得:
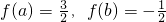
分析:(1)由
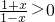 可得函数的定义域(-1,1),关于原点对称,再由
可得函数的定义域(-1,1),关于原点对称,再由 =
= 可判断函数奇偶性
可判断函数奇偶性(2)分别计算 f(a)+f(b)与
 可证
可证(3)由(2)
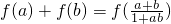 可得f(a)+f(b)=1
可得f(a)+f(b)=1 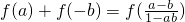 ,f(a)+f(b)=2结合奇函数的性质可得f(-b)=-f(b),从而可求
,f(a)+f(b)=2结合奇函数的性质可得f(-b)=-f(b),从而可求点评:本题主要考查了对数函数的定义域的求解,函数的奇欧性的判断及利用对数的基本运算性质证明等式,属于对数知识的综合应用.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目

 ,
, 上的单调性;
上的单调性; .
. ,求a,b的值.
,求a,b的值. .
. 的奇偶性;(4分)
的奇偶性;(4分) 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分) ,记
,记 ,试求函数
,试求函数 在区间
在区间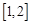 上的最大值.(10分)
上的最大值.(10分) .
. ,
, 的奇偶性;(2)求证:方程
的奇偶性;(2)求证:方程 至少有一根在区间
至少有一根在区间