题目内容
已知双曲线A.![]()
B.![]()
C.2
D.![]()
解析:方法一:由|PF1|-|PF2|=2a,|PF1|=4|PF2|得|PF2|=![]() a,|PF1|=
a,|PF1|=![]() a.
a.
由于|PF2|≥|F2A|,故![]() a≥c-a,
a≥c-a,
即e=![]() ≤
≤![]() .
.
方法二:同一,由于|PF1|+|PF2|≥|F1F2|,?
∴![]() a≥2c.∴e=
a≥2c.∴e=![]() ≤
≤![]() .?
.?
方法三:同一,设P(x,y),?
由于|PF2|=e(x-![]() )=
)=![]() a
a
![]() ex-a=
ex-a=![]() a
a![]() ex=
ex=![]() a
a![]() x=
x=![]() ,?
,?
由x≥a,知e≤![]() .
.
答案: B

练习册系列答案
相关题目


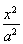

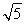
 -
- =1,椭圆的焦点恰好为双曲线的两个顶点,椭圆与双曲线的离心率互为倒数,则椭圆的方程为
.
=1,椭圆的焦点恰好为双曲线的两个顶点,椭圆与双曲线的离心率互为倒数,则椭圆的方程为
.