题目内容
已知 是
是 上的减函数,那么
上的减函数,那么 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
B
解析试题分析:根据题意,由于 是
是 上的减函数,则说明x<1时,3a-1<0,
上的减函数,则说明x<1时,3a-1<0, ,同时由于对数函数递减,则说明底数
,同时由于对数函数递减,则说明底数 ,同时要满足当x=1时,有3a-1+4a
,同时要满足当x=1时,有3a-1+4a ,故解得参数a的范围是
,故解得参数a的范围是 ,故选B.
,故选B.
考点:函数的单调性
点评:解决的冠关键是理解分段函数的单调性,要整体来分析,每段都是减函数,同时右边函数的最大值,要小于等于左边函数的最小值即可,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数 的零点个数为( )
的零点个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知函数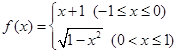 , 则
, 则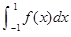 的值为
的值为
A. | B.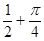 | C.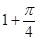 | D.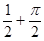 |
对于幂函数 ,若
,若 ,则
,则 ,
, 大小关系是( )
大小关系是( )
A.   | B.   |
C.   | D.无法确定 |
若 ,不等式
,不等式 的解集为
的解集为 ,关于
,关于 的不等式
的不等式 的解集记为
的解集记为 ,已知
,已知 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 单调递增,则关于x的不等式
单调递增,则关于x的不等式 的解集为 ( )
的解集为 ( )
A. | B. |
C.  | D.随a的值而变化 |
已知 ,
, ,…
,… 为凸多边形的内角,且
为凸多边形的内角,且 ,则这个多边形是( )
,则这个多边形是( )
| A.正六边形 | B.梯形 |
| C.矩形 | D.有一个角是锐角的菱形 |
方程 在区间
在区间 上有解,则实数
上有解,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B.  | C. | D. |
f(x)=-x2+mx在(-∞,1]上是增函数,则m的取值范围是( )
| A.{2} | B.(-∞,2] | C.[2,+∞) | D.(-∞,1] |