题目内容
f(x)=-x2+mx在(-∞,1]上是增函数,则m的取值范围是( )
| A.{2} | B.(-∞,2] | C.[2,+∞) | D.(-∞,1] |
C
解析试题分析:∵f(x)=-x2+mx在(-∞, ]上是增函数,∴要使在(-∞,1]上是增函数,只需
]上是增函数,∴要使在(-∞,1]上是增函数,只需 ,∴m≥2,故选C
,∴m≥2,故选C
考点:本题考查了函数单调性的运用
点评:一元二次函数的单调性的区分是根据其对称轴

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知 是
是 上的减函数,那么
上的减函数,那么 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
设函数 ,那么
,那么 ( )
( )
A. | B. | C. | D.1 |
已知函数f(x)= 在(-∞,+∞)上单调递减,那么实数a的取值范围是( )
在(-∞,+∞)上单调递减,那么实数a的取值范围是( )
| A.(0,1) | B. | C. | D. |
.函数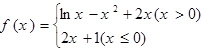 的零点的个数为( )
的零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
 ,则
,则 的大小关系是
的大小关系是
A. | B. | C. | D. |
若定义在R上的偶函数 上单调递减,且
上单调递减,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
对任意 ,函数
,函数 不存在极值点的充要条件是( )
不存在极值点的充要条件是( )
A. 或 或 | B. |
C. | D. 或 或 |
 ,则( )
,则( ) B.
B. 
 D.
D. 