题目内容
已知函数
是定义在
上的偶函数,且当
时,单调递增，则关于x的不等式
的解集为 （ ）
A． | B． |
C．  | D．随a的值而变化 |
C
解析试题分析：∵函数是定义在上的偶函数，∴1-a=2a，∴a=
，故函数的定义的定义域为
，又当
时,单调递增，∴
，解得
或
，所以不等式的解集为，故选C
考点：本题考查了抽象函数的运用
点评：此类问题往往利用偶函数的性质
避免了讨论，要注意灵活运用
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
个月的维修费为
元，买这种冰激凌机花费
元，使用
年报废，那么这台冰激凌机从投入使用到报废，每天的消耗是（ ）
机器从投入生产到报废共付出的维修费用与购买费用之和平均到每一天叫做每天的消耗;
一年按
天计算.）
元
元
元
元
的图象如右图所示，则m的值为
某人从2009年起，每年1月1日到银行新存入
元(一年定期)，若年利率为
保持不变，且每年到期存款和利息自动转为新的一年定期，到2012年底将所有存款及利息全部取回，则可取回的钱数（元)为
A． | B． | C． | D． |
已知
是
上的减函数，那么
的取值范围是 ( )
A． | B． | C． | D． |
若
，且
，则
的最大值是（ ）
| A．0 | B．1 | C．2 | D．4 |
不等式
的解集是
A． | B． |
| C． R | D． |
若直线
与幂函数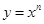
的图象相切于点
，则直线的方程为
A． | B． |
C． | D． |
，则（ ）
B. 
D. 