题目内容
记(bn)i=i+ +log2
+log2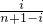 ,其中i,n∈N*,i≤n,如(bn)3=3+
,其中i,n∈N*,i≤n,如(bn)3=3+ +log2
+log2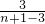 ,令Sn=(bn)1+(bn)2+(bn)3+…+(bn)n.
,令Sn=(bn)1+(bn)2+(bn)3+…+(bn)n.
(I)求(bn)1+(bn)n的值;
(Ⅱ)求Sn的表达式;
(Ⅲ)已知数列{an}满足Sn•an=1,设数列{an}的前n项和为Tn,若对一切n∈N*,不等式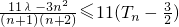 恒成立,求实数λ的最大值.
恒成立,求实数λ的最大值.
解:(I)∵(bn)i=i+ +log2
+log2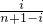 ,
,
∴(bn)1+(bn)n=(1+ +
+ )+(n+
)+(n+ )
)
=n+2+
=n+2.
(Ⅱ)∵Sn=(bn)1+(bn)2+(bn)3+…+(bn)n,
Sn=(bn)n+(bn)n-1+…+(bn)2+(bn)1,
∴2Sn=(bn)1+(bn)n+(bn)2+(bn)n-1+(bn)3+(bn)n-2+…+(bn)n+(bn)1
=n(n+2),
∴ .
.
(Ⅲ)∵ =
= ,
,
∴
= ,
,
当 ≤
≤ 恒成立.
恒成立.
∴
 恒成立,
恒成立,
∴11λ-3n2≤-11(2n+3)恒成立,
∴ 恒成立,
恒成立,
∴ ,
,
而 ,n∈N*.
,n∈N*.
∴n=4时, 取得最小值
取得最小值 .
.
∴ ,实数λ的最大值为
,实数λ的最大值为 .
.
分析:(I)由(bn)i=i+ +log2
+log2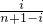 ,知(bn)1+(bn)n=(1+
,知(bn)1+(bn)n=(1+ +
+ )+(n+
)+(n+ ),由此能求出(bn)1+(bn)n=n+2.
),由此能求出(bn)1+(bn)n=n+2.
(Ⅱ)由Sn=(bn)1+(bn)2+(bn)3+…+(bn)n,知Sn=(bn)n+(bn)n-1+…+(bn)2+(bn)1,从而得到2Sn=(bn)1+(bn)n+(bn)2+(bn)n-1+(bn)3+(bn)n-2+…+(bn)n+(bn)1=n(n+2),由此能求出Sn的表达式.
(Ⅲ)由 =
= ,知
,知 =
= ,故
,故 ≤
≤ 恒成立,从而得到
恒成立,从而得到 ,由此能求出实数λ的最大值.
,由此能求出实数λ的最大值.
点评:本题考查数列与不等式的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点,易错点是 的推导.解题时要认真审题,仔细解答.
的推导.解题时要认真审题,仔细解答.
 +log2
+log2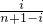 ,
,∴(bn)1+(bn)n=(1+
 +
+ )+(n+
)+(n+ )
)=n+2+

=n+2.
(Ⅱ)∵Sn=(bn)1+(bn)2+(bn)3+…+(bn)n,
Sn=(bn)n+(bn)n-1+…+(bn)2+(bn)1,
∴2Sn=(bn)1+(bn)n+(bn)2+(bn)n-1+(bn)3+(bn)n-2+…+(bn)n+(bn)1
=n(n+2),
∴
 .
.(Ⅲ)∵
 =
= ,
,∴

=
 ,
,当
 ≤
≤ 恒成立.
恒成立.∴

 恒成立,
恒成立,∴11λ-3n2≤-11(2n+3)恒成立,
∴
 恒成立,
恒成立,∴
 ,
,而
 ,n∈N*.
,n∈N*.∴n=4时,
 取得最小值
取得最小值 .
.∴
 ,实数λ的最大值为
,实数λ的最大值为 .
.分析:(I)由(bn)i=i+
 +log2
+log2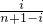 ,知(bn)1+(bn)n=(1+
,知(bn)1+(bn)n=(1+ +
+ )+(n+
)+(n+ ),由此能求出(bn)1+(bn)n=n+2.
),由此能求出(bn)1+(bn)n=n+2.(Ⅱ)由Sn=(bn)1+(bn)2+(bn)3+…+(bn)n,知Sn=(bn)n+(bn)n-1+…+(bn)2+(bn)1,从而得到2Sn=(bn)1+(bn)n+(bn)2+(bn)n-1+(bn)3+(bn)n-2+…+(bn)n+(bn)1=n(n+2),由此能求出Sn的表达式.
(Ⅲ)由
 =
= ,知
,知 =
= ,故
,故 ≤
≤ 恒成立,从而得到
恒成立,从而得到 ,由此能求出实数λ的最大值.
,由此能求出实数λ的最大值.点评:本题考查数列与不等式的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点,易错点是
 的推导.解题时要认真审题,仔细解答.
的推导.解题时要认真审题,仔细解答. 
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
已知某数列的前三项分别是下表第一、二、三行中的某一个数,且前三项中任何两个数不在下表的同一列.
若此数列是等差数列,记作{an},若此数列是等比数列,记作{bn}.
(I)求数列{an}和数列{bn}的通项公式;
(II)将数列{an}的项和数列{bn}的项依次从小到大排列得到数列{cn},数列{cn}的前n项和为Sn,试求最大的自然数M,使得当n≤M时,都有Sn≤2012.
(Ⅲ)若对任意n∈N,有an+1bn+λbnbn+1≥anbn+1成立,求实数λ的取值范围.
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 14 | 4 | 6 |
| 第三行 | 18 | 9 | 8 |
(I)求数列{an}和数列{bn}的通项公式;
(II)将数列{an}的项和数列{bn}的项依次从小到大排列得到数列{cn},数列{cn}的前n项和为Sn,试求最大的自然数M,使得当n≤M时,都有Sn≤2012.
(Ⅲ)若对任意n∈N,有an+1bn+λbnbn+1≥anbn+1成立,求实数λ的取值范围.
 +log2
+log2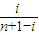 ,其中i,n∈N*,i≤n,如(bn)3=3+
,其中i,n∈N*,i≤n,如(bn)3=3+ +log2
+log2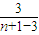 ,令Sn=(bn)1+(bn)2+(bn)3+…+(bn)n.
,令Sn=(bn)1+(bn)2+(bn)3+…+(bn)n.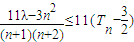 恒成立,求实数λ的最大值.
恒成立,求实数λ的最大值.