题目内容
设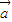 、
、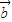 、
、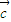 是三个非零向量,且
是三个非零向量,且 、
、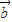 不共线,若关于x的方程
不共线,若关于x的方程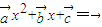 的两个根为x1,x2,则( )
的两个根为x1,x2,则( )A.x1>x2
B.x1=x2
C.x1<x2
D.x1,x2大小无法确定
【答案】分析:由题意可得 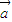 •
•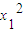 +
+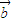 •x1+
•x1+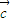 =0,
=0,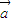 •
•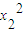 +
+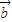 •x2+
•x2+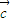 =0.把这两个等式相减可得 (x1-x2)[(x1+x2)
=0.把这两个等式相减可得 (x1-x2)[(x1+x2)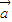 +
+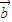 ]=0.由于(x1+x2)
]=0.由于(x1+x2)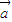 +
+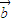 ≠0,可得 x1-x2=0.
≠0,可得 x1-x2=0.
解答:解:由于关于x的方程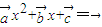 的两个根为x1,x2,故有
的两个根为x1,x2,故有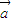 •
•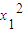 +
+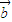 •x1+
•x1+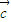 =0,
=0,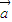 •
•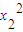 +
+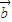 •x2+
•x2+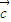 =0.
=0.
把这两个等式相减可得 (x1-x2)[(x1+x2)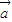 +
+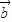 ]=0.
]=0.
由于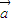 、
、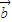 、
、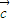 是三个非零向量,且
是三个非零向量,且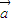 、
、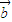 不共线,∴(x1+x2)
不共线,∴(x1+x2)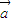 +
+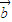 ≠0,∴x1-x2=0,
≠0,∴x1-x2=0,
故选B.
点评:本题主要考查两个向量共线的条件,得到(x1-x2)[(x1+x2)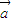 +
+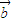 ]=0,是解题的关键,属于中档题.
]=0,是解题的关键,属于中档题.
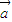 •
•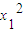 +
+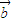 •x1+
•x1+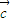 =0,
=0,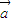 •
•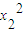 +
+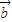 •x2+
•x2+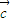 =0.把这两个等式相减可得 (x1-x2)[(x1+x2)
=0.把这两个等式相减可得 (x1-x2)[(x1+x2)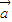 +
+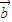 ]=0.由于(x1+x2)
]=0.由于(x1+x2)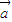 +
+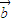 ≠0,可得 x1-x2=0.
≠0,可得 x1-x2=0.解答:解:由于关于x的方程
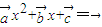 的两个根为x1,x2,故有
的两个根为x1,x2,故有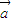 •
•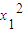 +
+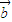 •x1+
•x1+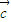 =0,
=0,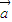 •
•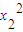 +
+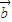 •x2+
•x2+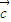 =0.
=0.把这两个等式相减可得 (x1-x2)[(x1+x2)
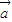 +
+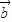 ]=0.
]=0.由于
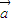 、
、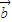 、
、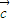 是三个非零向量,且
是三个非零向量,且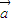 、
、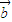 不共线,∴(x1+x2)
不共线,∴(x1+x2)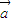 +
+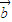 ≠0,∴x1-x2=0,
≠0,∴x1-x2=0,故选B.
点评:本题主要考查两个向量共线的条件,得到(x1-x2)[(x1+x2)
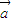 +
+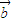 ]=0,是解题的关键,属于中档题.
]=0,是解题的关键,属于中档题. 
练习册系列答案
相关题目
设命题p:
,
,
是三个非零向量;命题q:{
,
,
}为空间的一组基,则命题q是命题p的( )
| a |
| b |
| c |
| a |
| b |
| c |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |