题目内容
【题目】点![]() 是直角
是直角![]() 斜边
斜边![]() 上一动点,
上一动点,![]()
![]() 将直角
将直角![]() 沿着
沿着![]() 翻折,使
翻折,使![]() 与
与![]() 构成直二面角,则翻折后
构成直二面角,则翻折后![]() 的最小值是_______.
的最小值是_______.
【答案】![]()
【解析】
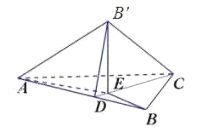
过点B′作B′E⊥CD于E,连结BE,AE,设∠BCD=∠B′CD=α,则有B′E=4sinα,CE=4cosα,![]() ,由此利用余弦定理、勾股定理能求出当
,由此利用余弦定理、勾股定理能求出当![]() 时,AB′取得最小值
时,AB′取得最小值![]() .
.
解:过点B′作B′E⊥CD于E,连结BE,AE,
设∠BCD=∠B′CD=α,
则有B′E=4sinα,CE=4cosα,![]() ,
,
在△AEC中,由余弦定理得:
![]()
=25+16cos2α﹣40sinαcosα,
在Rt△AEB′中,由勾股定理得:
AB'2=AE2+B′E2=25+16cos2α﹣40sinαcosα+16sin2α=41﹣20sin2α,
∴当![]() 时,AB′取得最小值
时,AB′取得最小值![]() .
.
故答案为:![]() .
.

【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 参数方程为
参数方程为![]() 为参数),将曲线
为参数),将曲线![]() 上所有点的横坐标变为原来的
上所有点的横坐标变为原来的![]() ,纵坐标变为原来的
,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 取得最小值时
取得最小值时![]() 的值.
的值.
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
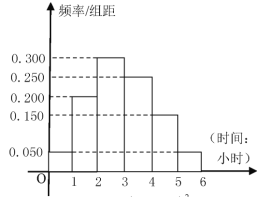
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附:
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
