题目内容
用一张矩形的纸片分别围成两个不同的圆柱形纸筒Ⅰ、Ⅱ，纸筒Ⅰ的侧面积为24π，纸筒Ⅱ的底面半径为3，则纸筒的Ⅱ的容积为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：计算题
分析：由纸筒I的侧面积，可知纸筒II的侧面积，再由纸筒II的底面半径为3．可求得纸筒II的母线长，代入体积公式计算．
解答：
解：根据纸筒I与纸筒II的侧面积相同，设纸筒II的母线长为L，
∴24π=2π×3×L⇒L=4，
∴纸筒II的容积V=π32×4=36π．
故答案是36π．
∴24π=2π×3×L⇒L=4，
∴纸筒II的容积V=π32×4=36π．
故答案是36π．
点评：本题考查了圆柱的侧面积公式及应用，圆柱的侧面积S=2πrL．
练习册系列答案
相关题目
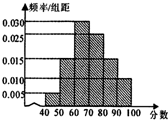某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]加以统计，得到如图所示的频率分布直方图，已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为已知正四面体ABCD的棱长为2，所有与它的四个顶点距离相等的平面截这个四面体所得截面的面积之和是
（ ）
（ ）
A、3+
| ||
| B、4 | ||
| C、3 | ||
D、
|