题目内容
如图，已知点
是边长为1的等边
的中心，则
等于（
）
A．
B．
C．
D．
【答案】
D
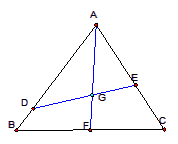
【解析】解：因为点O是边长为1的等边△ABC的中心，D为BC的中点， OA ， OC ， OB 两两夹角为120°．
所以| OA |=| OB |=| OC |=2 /3 |AD|=2 /3 ×
/ 2 = / 3 ．
所以（ OA + OB ）•（ OA + OC ）
= OA 2+ OB • OA + OA • OC + OB •
OC=( /
3 )2+( / 3 )2cos120°+( /
3 )2cos120°+( / 3 )2cos120°
=( / 3 )2 (1+3cos120°)
=-1/ 6 ．
故选D．
练习册系列答案
名校课堂系列答案
相关题目
是边长为
的正三角形
的中心，线段
经过点
、
于点
、
；设
，
，其中
，
．
的值，并说明理由；
面积的最大和最小值，并指出相应的
、
的值．
（本题满分16分，第（1）小题6分，第（2）小题10分）
是边长为
的正三角形
的中心，线段
经过点
、
于点
、
；设
，
，其中
，
．
的值，并说明理由；
面积的最大和最小值，并指出相应的
、
的值．
是边长为1的等边
的中心，则
等于（ ）
B．
C．
D．
是边长为1的等边
的中心，则
等于（
）
B．
C．
D．
