题目内容
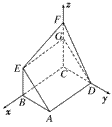
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF且BE<CF,∠BCF= ,AD=
,AD= ,EF=2。
,EF=2。
 ,AD=
,AD= ,EF=2。
,EF=2。
(1)求证:AE∥平面DCF;
(2)设 =λ,当λ取何值时,二面角A-EF-C的大小为
=λ,当λ取何值时,二面角A-EF-C的大小为 。
。
(2)设
 =λ,当λ取何值时,二面角A-EF-C的大小为
=λ,当λ取何值时,二面角A-EF-C的大小为 。
。| 解:(1)证明:∵四边形ABCD是矩形, ∴AB∥DC 又BE∥CF,AB∩BE=B, ∴平面ABE∥平面DCF 又AE 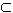 平面ABE, 平面ABE, ∴AE∥平面DCF。 |
|
| (2)过点E作GE⊥CF交CF于点G, 由已知可得:EG∥BC∥AD,且EG=BC=AD, ∴EG=AD= 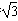 , ,又EF=2, ∴GF=1 ∵四边形ABCD是矩形, ∴DC⊥BC ∵∠BCF= 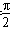 , ,∴FC⊥BC, 又平面ABCD⊥平面BEFC,平面ABCD∩平面BEFC=BC ∴FC⊥平面ABCD, ∴FC⊥CD ∴分别以C为原点,CB、CD、CF所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系 设BE=m 由 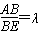 得AB=λm 得AB=λm∴A( 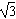 ,λm,0),E( ,λm,0),E(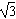 ,0,m),F(0,0,m+1) ,0,m),F(0,0,m+1)∴ 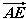 =(0,-λm,m), =(0,-λm,m),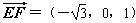 设平面AEF的法向量为n=(x,y,z) 由 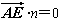 , ,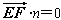 得 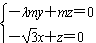 ∴ 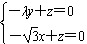 令y= 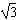 可得平面AEF的一个法向量n=(λ, 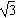 , ,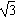 λ) λ)又 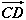 =(0,λm,0)是平面CEF的一个法向量 =(0,λm,0)是平面CEF的一个法向量∴ 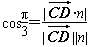 即 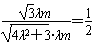 解得 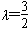 ∴当 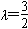 时,二面角A-EF-C的大小为 时,二面角A-EF-C的大小为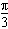 。 。 |
 |

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
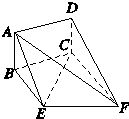 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF= 如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,
如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°, 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD= 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=