题目内容
2.已知函数y=x2定义域为A,值域为{1,4,9}.这样的A有多少个?分析 根据值域中的几个函数值,结合函数表达式推断出定义域中可能出现的几个x值,再加以组合即可得到定义域A的各种情况.
解答 解:函数y=x2定义域为A,值域为{1,4,9},
∴x2=1,x2=4,x2=9,
∴x=±1,±2,±3,
各取1个有C21C21C21=8个,
其中一个取1个,另外两个都取2个,有C31C21=6个,
其中一个取2个,另外两个都取1个,有C31C21C21=12个,
各取2个,有1种,
故共有8+6+12+1=27个.
点评 本题给出二次函数的一个值域,要我们求函数的定义域最多有几个,着重考查了函数的定义与进行简单合情推理等知识,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.不等式3x-2y-6<0表示的区域在直线3x-2y-6=0的( )
| A. | 右上方 | B. | 右下方 | C. | 左上方 | D. | 左下方 |
16.圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
| A. | $\frac{\sqrt{7}}{3}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{2}{5}\sqrt{7}$ | D. | $\sqrt{7}$ |
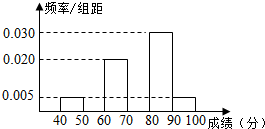 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,