题目内容
定义x1,x2,…,xn的“倒平均数”为
(n∈N*).
(1)若数列{an}前n项的“倒平均数”为
,求{an}的通项公式;
(2)设数列{bn}满足:当n为奇数时,bn=1,当n为偶数时,bn=2.若Tn为{bn}前n项的倒平均数,求
Tn;
(3)设函数f(x)=-x2+4x,对(1)中的数列{an},是否存在实数λ,使得当x≤λ时,f(x)≤
对任意n∈N*恒成立?若存在,求出最大的实数λ;若不存在,说明理由.
| n |
| x1+x2+…+xn |
(1)若数列{an}前n项的“倒平均数”为
| 1 |
| 2n+4 |
(2)设数列{bn}满足:当n为奇数时,bn=1,当n为偶数时,bn=2.若Tn为{bn}前n项的倒平均数,求
| lim |
| n→∞ |
(3)设函数f(x)=-x2+4x,对(1)中的数列{an},是否存在实数λ,使得当x≤λ时,f(x)≤
| an |
| n+1 |
(1)设数列{an}的前n项和为Sn,
由题意,Tn=
=
,
所以Sn=2n2+4n. …(1分)
所以a1=S1=6,当n≥2时,an=Sn-Sn-1=4n+2,
而a1也满足此式.…(2分)
所以{an}的通项公式为an=4n+2.…(1分)
(2)设数列{bn}的前n项和为Sn,则当n为偶数时,Sn=
,…(1分)
当n为奇数时,Sn=
+1=
. …(1分)
所以Tn=
. …(3分)
所以
Tn=
. …(2分)
(3)假设存在实数λ,使得当x≤λ时,f(x)≤
对任意n∈N*恒成立,
则-x2+4x≤
对任意n∈N*恒成立,…(1分)
令cn=
,因为cn+1-cn=
>0,
所以数列{cn}是递增数列,…(1分)
所以只要-x2+4x≤c1,即x2-4x+3≥0,
解得x≤1或x≥3.…(2分)
所以存在最大的实数λ=1,
使得当x≤λ时,f(x)≤
对任意n∈N*恒成立.(2分)
由题意,Tn=
| n |
| Sn |
| 1 |
| 2n+4 |
所以Sn=2n2+4n. …(1分)
所以a1=S1=6,当n≥2时,an=Sn-Sn-1=4n+2,
而a1也满足此式.…(2分)
所以{an}的通项公式为an=4n+2.…(1分)
(2)设数列{bn}的前n项和为Sn,则当n为偶数时,Sn=
| 3n |
| 2 |
当n为奇数时,Sn=
| 3(n-1) |
| 2 |
| 3n-1 |
| 2 |
所以Tn=
|
所以
| lim |
| n→∞ |
| 2 |
| 3 |
(3)假设存在实数λ,使得当x≤λ时,f(x)≤
| an |
| n+1 |
则-x2+4x≤
| 4n+2 |
| n+1 |
令cn=
| 4n+2 |
| n+1 |
| 2 |
| (n+1)(n+2) |
所以数列{cn}是递增数列,…(1分)
所以只要-x2+4x≤c1,即x2-4x+3≥0,
解得x≤1或x≥3.…(2分)
所以存在最大的实数λ=1,
使得当x≤λ时,f(x)≤
| an |
| n+1 |

练习册系列答案
相关题目
 (n∈N*).
(n∈N*). ,求{an}的通项公式;
,求{an}的通项公式; ;
; 对任意n∈N*恒成立?若存在,求出最大的实数λ;若不存在,说明理由.
对任意n∈N*恒成立?若存在,求出最大的实数λ;若不存在,说明理由.  (n∈N*).已知数列{an}前n项的“倒平均数”为
(n∈N*).已知数列{an}前n项的“倒平均数”为 ,记cn=
,记cn= (n∈N*).
(n∈N*). Tn.
Tn.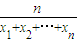 (n∈N*).
(n∈N*).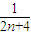 ,求{an}的通项公式;
,求{an}的通项公式;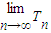 ;
;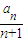 对任意n∈N*恒成立?若存在,求出最大的实数λ;若不存在,说明理由.
对任意n∈N*恒成立?若存在,求出最大的实数λ;若不存在,说明理由.