��Ŀ����
����x1��x2������xn�ġ���ƽ������Ϊ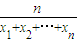 ��n��N*����
��n��N*������1��������{an}ǰn��ġ���ƽ������Ϊ
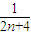 ����{an}��ͨ�ʽ��
����{an}��ͨ�ʽ����2��������{bn}���㣺��nΪ����ʱ��bn=1����nΪż��ʱ��bn=2����TnΪ{bn}ǰn��ĵ�ƽ��������
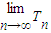 ��
����3���躯��f��x��=-x2+4x���ԣ�1���е�����{an}���Ƿ����ʵ���ˣ�ʹ�õ�x�ܦ�ʱ��f��x����
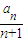 ������n��N*������������ڣ��������ʵ���ˣ��������ڣ�˵�����ɣ�
������n��N*������������ڣ��������ʵ���ˣ��������ڣ�˵�����ɣ�
���𰸡���������1��������{an}��ǰn���ΪSn�������⣬ ������
������ ���ɴ������{an}��ͨ�ʽ��
���ɴ������{an}��ͨ�ʽ��
��2��������{bn}��ǰn���ΪSn�����nΪż����nΪ����ʱ���ֱ����Sn���Ӷ����Tn���ɴ������ ��
��
��3���������ʵ���ˣ�ʹ�õ�x�ܦ�ʱ��f��x�� ������n��N*���������-x2+4x��
������n��N*���������-x2+4x�� ������n��N*���������
������n��N*��������� ��������{cn}�ǵ������У��ɴ����Ƶ�����������ʵ����=1��ʹ�õ�x�ܦ�ʱ��f��x��
��������{cn}�ǵ������У��ɴ����Ƶ�����������ʵ����=1��ʹ�õ�x�ܦ�ʱ��f��x�� ������n��N*�������
������n��N*�������
����⣺��1��������{an}��ǰn���ΪSn��
�����⣬ ��
��
���� �� ����1�֣�
�� ����1�֣�
����a1=S1=6����n��2ʱ��an=Sn-Sn-1=4n+2��
��a1Ҳ�����ʽ������2�֣�
����{an}��ͨ�ʽΪan=4n+2������1�֣�
��2��������{bn}��ǰn���ΪSn����nΪż��ʱ�� ������1�֣�
������1�֣�
��nΪ����ʱ�� �� ����1�֣�
�� ����1�֣�
���� �� ����3�֣�
�� ����3�֣�
����
 �� ����2�֣�
�� ����2�֣�
��3���������ʵ���ˣ�ʹ�õ�x�ܦ�ʱ��f��x�� ������n��N*�������
������n��N*�������
��-x2+4x�� ������n��N*�����������1�֣�
������n��N*�����������1�֣�
�� ����Ϊ
����Ϊ ��
��
��������{cn}�ǵ������У�����1�֣�
����ֻҪ-x2+4x��c1����x2-4x+3��0��
���x��1��x��3������2�֣�
���Դ�������ʵ����=1��
ʹ�õ�x�ܦ�ʱ��f��x�� ������n��N*���������2�֣�
������n��N*���������2�֣�
���������⿼�����е�ͨ�ʽ��������̽��ʵ���Ƿ���ڣ��ۺ���ǿ���Ѷȴ���һ����̽���ԣ�����ѧ˼ά��Ҫ��ϸߣ�����ʱҪ�������⣬��ϸ���
 ������
������ ���ɴ������{an}��ͨ�ʽ��
���ɴ������{an}��ͨ�ʽ����2��������{bn}��ǰn���ΪSn�����nΪż����nΪ����ʱ���ֱ����Sn���Ӷ����Tn���ɴ������
 ��
����3���������ʵ���ˣ�ʹ�õ�x�ܦ�ʱ��f��x��
 ������n��N*���������-x2+4x��
������n��N*���������-x2+4x�� ������n��N*���������
������n��N*��������� ��������{cn}�ǵ������У��ɴ����Ƶ�����������ʵ����=1��ʹ�õ�x�ܦ�ʱ��f��x��
��������{cn}�ǵ������У��ɴ����Ƶ�����������ʵ����=1��ʹ�õ�x�ܦ�ʱ��f��x�� ������n��N*�������
������n��N*�����������⣺��1��������{an}��ǰn���ΪSn��
�����⣬
 ��
������
 �� ����1�֣�
�� ����1�֣�����a1=S1=6����n��2ʱ��an=Sn-Sn-1=4n+2��
��a1Ҳ�����ʽ������2�֣�
����{an}��ͨ�ʽΪan=4n+2������1�֣�
��2��������{bn}��ǰn���ΪSn����nΪż��ʱ��
 ������1�֣�
������1�֣���nΪ����ʱ��
 �� ����1�֣�
�� ����1�֣�����
 �� ����3�֣�
�� ����3�֣�����

 �� ����2�֣�
�� ����2�֣���3���������ʵ���ˣ�ʹ�õ�x�ܦ�ʱ��f��x��
 ������n��N*�������
������n��N*���������-x2+4x��
 ������n��N*�����������1�֣�
������n��N*�����������1�֣���
 ����Ϊ
����Ϊ ��
����������{cn}�ǵ������У�����1�֣�
����ֻҪ-x2+4x��c1����x2-4x+3��0��
���x��1��x��3������2�֣�
���Դ�������ʵ����=1��
ʹ�õ�x�ܦ�ʱ��f��x��
 ������n��N*���������2�֣�
������n��N*���������2�֣����������⿼�����е�ͨ�ʽ��������̽��ʵ���Ƿ���ڣ��ۺ���ǿ���Ѷȴ���һ����̽���ԣ�����ѧ˼ά��Ҫ��ϸߣ�����ʱҪ�������⣬��ϸ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��n��N*����
��n��N*���� ����{an}��ͨ�ʽ��
����{an}��ͨ�ʽ�� ��
�� ������n��N*������������ڣ��������ʵ���ˣ��������ڣ�˵�����ɣ�
������n��N*������������ڣ��������ʵ���ˣ��������ڣ�˵�����ɣ�  ��n��N*������֪����{an}ǰn��ġ���ƽ������Ϊ
��n��N*������֪����{an}ǰn��ġ���ƽ������Ϊ ����cn=
����cn= ��n��N*����
��n��N*���� Tn��
Tn��