题目内容
 的角
的角 的对边分别为
的对边分别为 ,已知
,已知 .
.
(Ⅰ)求角 ;
;
(Ⅱ)若 ,
, ,求
,求 的值.
的值.
(Ⅰ)  ;(Ⅱ)
;(Ⅱ)  .
.
解析试题分析:(Ⅰ)先根据正弦定理将已知表达式: ,全部转化为边的关系,然后根据余弦定理求出角
,全部转化为边的关系,然后根据余弦定理求出角 的余弦值,结合特殊角的三角函数值以及三角形的内角求角
的余弦值,结合特殊角的三角函数值以及三角形的内角求角 ;(Ⅱ)先根据三三角形的面积公式求出
;(Ⅱ)先根据三三角形的面积公式求出 ,然后根据余弦定理的变形,求得
,然后根据余弦定理的变形,求得 ,
,
将已知的 与
与 代入此式可解得
代入此式可解得 .
.
试题解析:(1)根据正弦定理 ,原等式可转化为:
,原等式可转化为: , 2分
, 2分 , 4分
, 4分
∴ . 6分
. 6分
(Ⅱ) ,
,
∴ , 8分
, 8分 , 10分
, 10分
∴ . 12分
. 12分
考点:1.正弦定理;2.余弦定理及其变形;3.解三角形;4.三角形的面积公式;5.特殊角的三角函数值

练习册系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, 的大小;
的大小; ,求
,求 的顶点
的顶点 ,顶点
,顶点 在直线
在直线 上;
上; 求点
求点 ,且
,且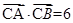 ,求角
,求角 中,满足
中,满足 的夹角为
的夹角为 ,
, 是
是 的中点,
的中点,  ,求向量
,求向量 的夹角的余弦值;.
的夹角的余弦值;. ,点
,点 在边
在边 上且
上且 ,如果
,如果 ,求
,求 的值。
的值。 中,角
中,角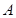 、
、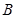 、
、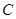 的对边分别为
的对边分别为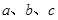 ,且
,且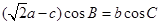 .
.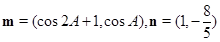 ,且
,且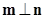 ,求
,求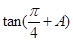 的值.
的值.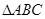 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足
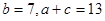 ,求
,求 的取值范围.
的取值范围. 的外接圆半径
的外接圆半径 ,角
,角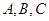 的对边分别是
的对边分别是 ,且
,且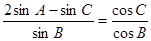
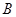 和边长
和边长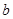 ;
;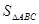 的最大值及取得最大值时的
的最大值及取得最大值时的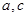 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状. ,且C=120°.
,且C=120°. 中,
中, 边上的中线
边上的中线 长为3,且
长为3,且 ,
, .
.
 的值;(Ⅱ)求
的值;(Ⅱ)求 边的长.
边的长.