题目内容
有下列数组排成一排: 如果把上述数组中的括号都去掉会形成一个数列:
如果把上述数组中的括号都去掉会形成一个数列: 则此数列中的第2011项是
则此数列中的第2011项是
- A.

- B.

- C.
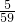
- D.

B
分析:观察数列:
知此数列的项数共有1+2+3+4+5+…+n项,项数和为 ,求此数列的第2011项时,验证,知
,求此数列的第2011项时,验证,知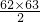 =1953,
=1953,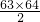 =2016,则该项分母为2011-1953=58,分子为63-58+1=6,从而求得该数列的第2011项.
=2016,则该项分母为2011-1953=58,分子为63-58+1=6,从而求得该数列的第2011项.
解答:观察数列:
知此数列:
项数是1+2+3+4+5+…+n组成,项数和为 ,求此数列中的第2011项时,验证,知
,求此数列中的第2011项时,验证,知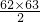 =1953,
=1953,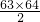 =2016,所以,该项的分母为2011-1953=58,分子为63-58+1=6;所以,数列的第2011项是
=2016,所以,该项的分母为2011-1953=58,分子为63-58+1=6;所以,数列的第2011项是 .
.
故应选:B.
点评:本题考查了等差数列的综合运用,在求数列中的第2011项时,先确定 ≥2011,且
≥2011,且 ≤2011时n的值,再确定该项分母,分子的值,较为容易.
≤2011时n的值,再确定该项分母,分子的值,较为容易.
分析:观察数列:

知此数列的项数共有1+2+3+4+5+…+n项,项数和为
 ,求此数列的第2011项时,验证,知
,求此数列的第2011项时,验证,知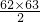 =1953,
=1953,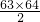 =2016,则该项分母为2011-1953=58,分子为63-58+1=6,从而求得该数列的第2011项.
=2016,则该项分母为2011-1953=58,分子为63-58+1=6,从而求得该数列的第2011项.解答:观察数列:

知此数列:

项数是1+2+3+4+5+…+n组成,项数和为
 ,求此数列中的第2011项时,验证,知
,求此数列中的第2011项时,验证,知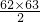 =1953,
=1953,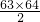 =2016,所以,该项的分母为2011-1953=58,分子为63-58+1=6;所以,数列的第2011项是
=2016,所以,该项的分母为2011-1953=58,分子为63-58+1=6;所以,数列的第2011项是 .
.故应选:B.
点评:本题考查了等差数列的综合运用,在求数列中的第2011项时,先确定
 ≥2011,且
≥2011,且 ≤2011时n的值,再确定该项分母,分子的值,较为容易.
≤2011时n的值,再确定该项分母,分子的值,较为容易. 
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如果把上述数组中的括号都去掉会形成一个数列:
如果把上述数组中的括号都去掉会形成一个数列: 则此数列中的第2012项是 。
则此数列中的第2012项是 。
 则此数列中的第
则此数列中的第 项是
项是 B.
B. C.
C. D.
D.