题目内容
4．在数列$\sqrt{2}$，2，x，2$\sqrt{2}$，$\sqrt{10}$，2$\sqrt{3}$，…中，x=$\sqrt{6}$．分析 通过观察可知，数列$\sqrt{2}$，2，x，2$\sqrt{2}$，$\sqrt{10}$，2$\sqrt{3}$，…即为$\sqrt{2}$，$\sqrt{4}$，x，$\sqrt{8}$，$\sqrt{10}$，$\sqrt{12}$，…，即可求出x的值．
解答 解：数列$\sqrt{2}$，2，x，2$\sqrt{2}$，$\sqrt{10}$，2$\sqrt{3}$，…即为$\sqrt{2}$，$\sqrt{4}$，x，$\sqrt{8}$，$\sqrt{10}$，$\sqrt{12}$，…，
故x=$\sqrt{6}$，
故答案为：$\sqrt{6}$．
点评 本题考查了数列的概念及简单表示法，主要借助数列的概念考查学生的观察能力，属于基础题型．
练习册系列答案
相关题目
14．已知θ为第一象限角，设$\overrightarrow a=（\sqrt{3}，-sinθ）$，$\overrightarrow b=（cosθ，3）$，且$\overrightarrow a⊥\overrightarrow b$，则θ一定为（ ）
| A． | $\frac{π}{3}+kπ（k∈Z）$ | B． | $\frac{π}{6}+2kπ（k∈Z）$ | C． | $\frac{π}{3}+2kπ（k∈Z）$ | D． | $\frac{π}{6}+kπ（k∈Z）$ |
15．记集合M={（x，y）|（x-2cosθ）2+（y-2sinθ）2＜1}，任取点P∈M，则点P∈{（x，y）|x2+y2≤4}的概率（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{4}{9}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{3}$ |
12．设x，y满足$\left\{\begin{array}{l}{y≥0}\\{ax+y-1≤0}\\{3x-2y-2≤0}\end{array}\right.$，若z=x2-10x+y2的最小值为-12，实数a的取值范围是（ ）
| A． | a$≤-\frac{1}{2}$ | B． | a$≤-\frac{3}{2}$ | C． | a$≥\frac{1}{2}$ | D． | a$＜\frac{3}{2}$ |
9．函数y=$\frac{1}{2}$cosx，x∈[-$\frac{π}{3}$，$\frac{2π}{3}$]的值域是（ ）
| A． | [-1，$\frac{1}{2}$] | B． | [-$\frac{1}{4}$，$\frac{1}{2}$] | C． | [-$\frac{\sqrt{3}}{4}$，$\frac{1}{4}$] | D． | [-$\frac{1}{2}$，1] |
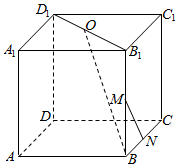如图，正方体ABCD-A1B1C1D1中，M、N、O分别为BB1，BC，B1D1的中点，求异面直线OB与MN所成角的余弦值．