题目内容

lim
n→∞
(
1
12+2
+
1
22+4
+
1
32+6
+…+
1
n2+2n
)=
 
．
分析：由
1
n2+2n
=
1
n(n+2)
=
1
2
(
1
n
-
1
n+2
)，知
lim
n→∞
(
1
12+2
+
1
22+4
+
1
32+6
+…+
1
n2+2n
)=
1
2
lim
n→∞
  (1+
1
2
-
1
n+2
)，由此能导出其最终结果．
解答：解：∵
1
n2+2n
=
1
n(n+2)
=
1
2
(
1
n
-
1
n+2
)，
∴
lim
n→∞
(
1
12+2
+
1
22+4
+
1
32+6
+…+
1
n2+2n
)
=
1
2
lim
n→∞
[(1-
1
3
)+(
1
2
-
1
4
)+(
1
3
-
1
5
)+(
1
4
-
1
6
)+…+(
1
n
-
1
n+2
)]
=
1
2
lim
n→∞
  (1+
1
2
-
1
n+2
)
=
3
4
．
故答案为：
3
4
．
点评：本题考查数列的极限和性质，解题时要注意裂项求和公式的合理运用．
练习册系列答案
相关题目
精英家教网将杨辉三角中的每一个数Cnr都换成
1
(n+1)
C
r
n
，就得到一个如下图所示的分数三角形，成为莱布尼茨三角形，从莱布尼茨三角形可看出
1
(n+1)
C
r
n
+
1
(n+1)
C
x
n
=
1
n
C
r
n-1
，其中x=r+1，令an=
1
3
+
1
12
+
1
30
+
1
60
+…+
1
n
C
2
n-1
+
1
(n+1)
C
2
n
，则
lim
n→∞
an=
 
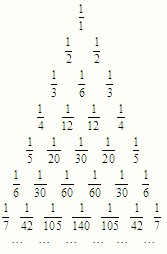将杨晖三角形中的每一个数Cnr都换成分数 
1
(n+1)
C
r
n
，就得到一个如图所示的分数三角形，称为莱布尼兹三角形．令an=
1
3
+
1
12
+
1
30
+
1
60
+…+
1
n
C
n-3
n-1
+
1
(n+1)
C
n-2
n
，
观察莱布尼兹三角形规律，计算极限
lim
n→∞
an=
1
2
1
2
．
（2006•广州二模）若Sn=
1
12+2
+
1
22+4
+
1
32+6
+…+
1
n2+2n
（n∈N*），则
lim
n→∞
Sn=
3
4
3
4
．
已知等差数列{an}公差不为0，其前n项和为Sn，等比数列{bn}前n项和为Bn，公比为q，且|q|＞1，则
lim
n→+∞
(
Sn
nan
+
Bn
bn
)=
1
2
+
q
q-1
1
2
+
q
q-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网