题目内容
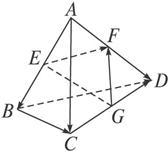
如右图,已知空间四边形ABCD的每条边和对角线的长都等于a,点M,N分别是边AB,CD的中点.
(1)求证:MN为AB和CD的公垂线;
(2)求MN的长;
(3)求异面直线AN与MC所成角的余弦值.
解:设![]() =p,
=p,![]() =q,
=q,![]() =r,
=r,
(1)证明:![]() =
=![]() (
(![]() )-
)-![]()
![]()
=![]() (q+r-p),
(q+r-p),
所以![]() ·
·![]() =
=![]() (q+r-p)·p=
(q+r-p)·p=![]() (q·p+r·p-p2)=
(q·p+r·p-p2)=![]() (a2·cos60°+a2·cos60°-a2)=0.
(a2·cos60°+a2·cos60°-a2)=0.
所以MN⊥AB,同理可证MN⊥CD.
所以MN为AB与CD的公垂线.
(2)解:由(1)可知![]() =
=![]() (q+r-p),
(q+r-p),
所以|![]() |2=(
|2=(![]() )2=
)2=![]() (q+r-p)2=
(q+r-p)2=![]() [q2+r2+p2+2(q·r-q·p-r·p)]=
[q2+r2+p2+2(q·r-q·p-r·p)]=![]() [a2+a2+a2+2(
[a2+a2+a2+2(![]() -
-![]() -
-![]() )]=
)]=![]() ×2a2=
×2a2=![]() .
.
所以|![]() |=
|=![]() a.
a.
所以MN的长度为![]() a.
a.
(3)解:设向量![]() 与
与![]() 的夹角为θ,
的夹角为θ,
因为![]() =
=![]() (
(![]() )=
)=![]() (q+r),
(q+r),
![]() =
=![]() -
-![]() =q-
=q-![]() p,
p,
所以![]() ·
·![]() =
=![]() (q+r)·(q-
(q+r)·(q-![]() p)
p)
=![]() (q2-
(q2-![]() q·p+r·q-
q·p+r·q-![]() r·p)
r·p)
=![]() (a2-
(a2-![]() a2·cos60°+a2cos60°-
a2·cos60°+a2cos60°-![]() a2·cos60°)
a2·cos60°)
=![]() (a2-
(a2-![]() +
+![]() -
-![]() )=
)=![]() .
.
又因为|![]() |=|
|=|![]() |=
|=![]() a,
a,
所以![]() ·
·![]() =|
=|![]() |·|
|·|![]() |·cosθ
|·cosθ
=![]() a·
a·![]() a·cosθ=
a·cosθ=![]() .
.
所以cosθ=![]() .
.
所以向量![]() 与
与![]() 的夹角余弦值为
的夹角余弦值为![]() .
.
从而异面直线AN,MC所成角的余弦值为![]() .
.

练习册系列答案
相关题目