题目内容
已知函数f(x)＝x(ln x－ax)有两个极值点，则实数a的取值范围是( )
A．(－∞，0) B．(0，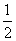
)
C．(0,1) D．(0，＋∞)
B
解析 
函数f(x)＝x(ln x－ax)的定义域为(0，＋∞)，且f′(x)＝ln x－ax＋x(
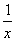－a)＝ln x－2ax＋1.如果函数f(x)＝x(ln x－ax)有两个极值点，也就是说f′(x)＝0有两个不等实根，即ln x－2ax＋1＝0有两个不等实根．参数分离得
＝2a，若此方程有两个不等实根，只需函数y＝
与y＝2a有两个不同交点．经过求导分析，如图所示，可知0<2a<1，则0<a<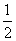.故选B.
练习册系列答案
相关题目
的前n项和．
B．
D．
和曲线
所围成的图形的面积为________.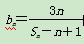
的前n项和为Tn，证明：Tn<6.
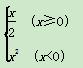， 则f[f(x)]≥1的充要条件是( )
]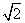